FRANK Solutions for Class 9 Maths Chapter 19 - Quadrilaterals

FRANK Solutions for Class 9 Maths Chapter 19 - Quadrilaterals

Chapter 19 - Quadrilaterals Exercise Ex. 19.1

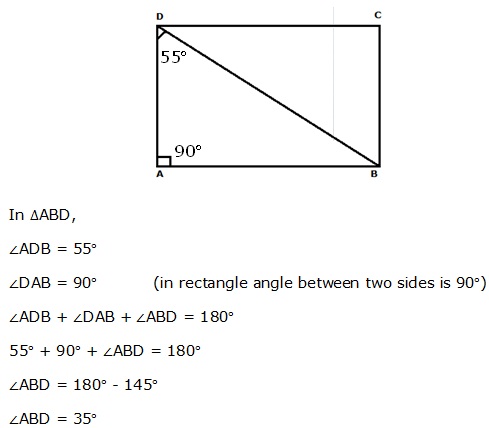
Question 1

In the following figures, find the remaining angles of the  parallelogram

Solution 1

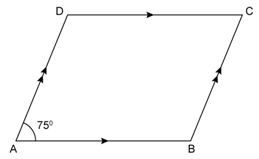
Question 2

In the following figures, find the remaining angles of the  parallelogram

Solution 2

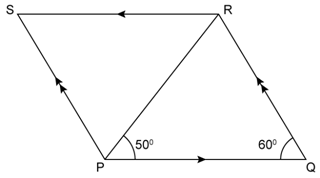
Question 3

In the following figures, find the remaining angles of the  parallelogram

Solution 3

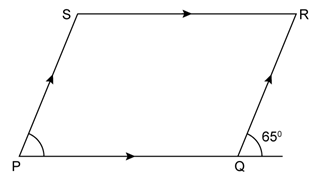
Question 4

In the following figures, find the remaining angles of the  parallelogram

Solution 4

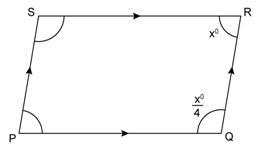
Question 5

In the following figures, find the remaining angles of the  parallelogram

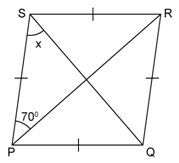
Solution 5

Question 6

Solution 6

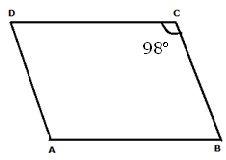
Question 7

The consecutive angles of a parallelogram are in the ratio 3:6. Calculate the measures of all the angles of the parallelogram.

Solution 7

Question 8

Solution 8

Question 9

In the given figure, ABCD is a parallelogram, find the values of x and y.

Solution 9

Question 10

Solution 10

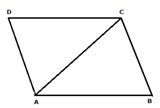
Question 11

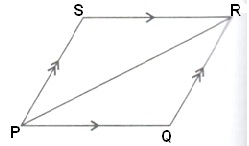
Solution 11

Question 12

Solution 12

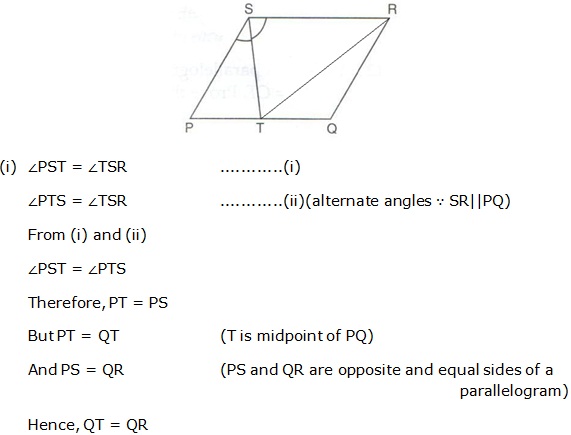
Question 13

Solution 13

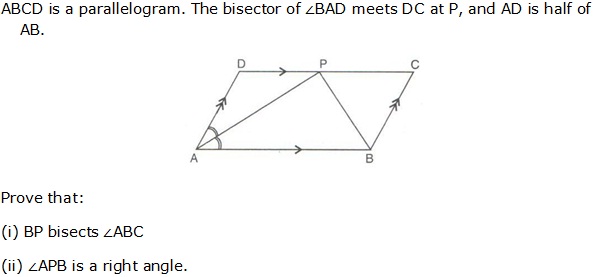
Question 14

Solution 14

Question 15

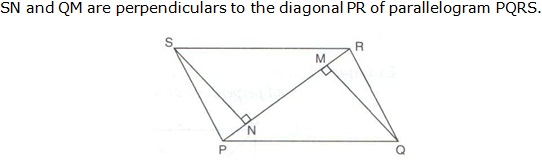
Solution 15

Question 16

Solution 16

Question 17

In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.

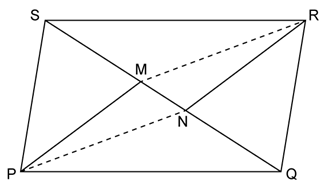
Solution 17

Construction: Join PR.

Question 18

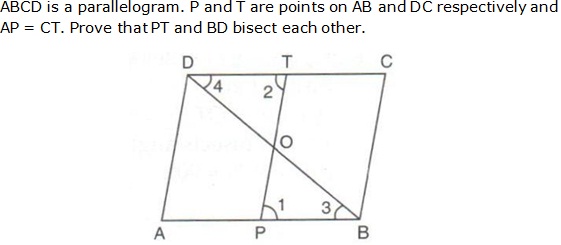
Solution 18

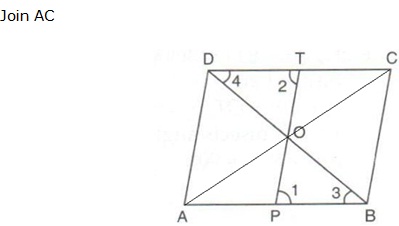
Question 19

Solution 19

Chapter 19 - Quadrilaterals Exercise Ex. 19.2

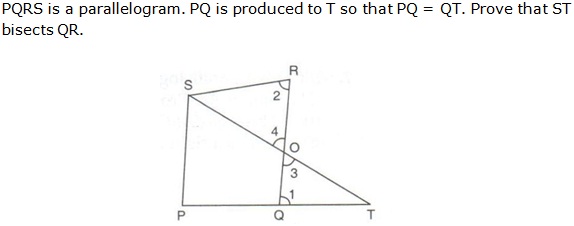
Question 1

Solution 1

Question 2

Solution 2

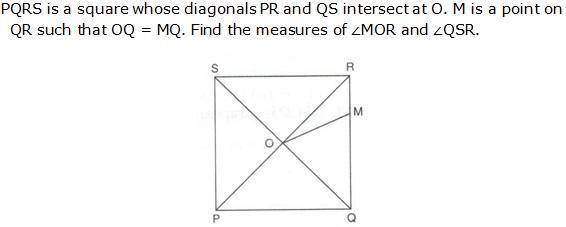
Question 3

Solution 3

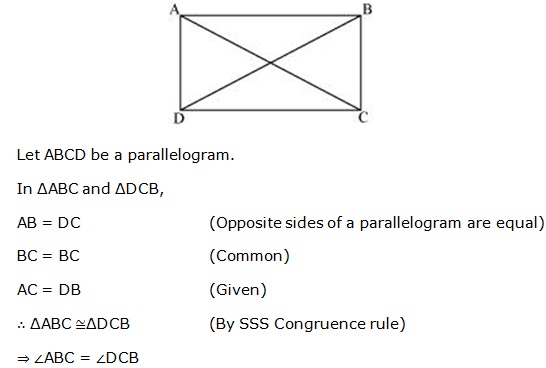
Question 4

Solution 4

Question 5

Solution 5

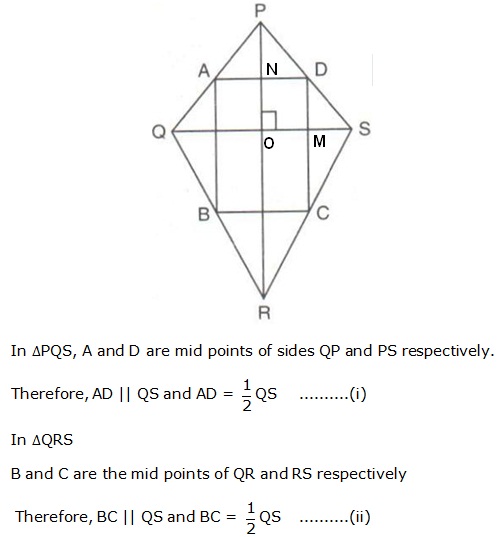
Question 6

Solution 6

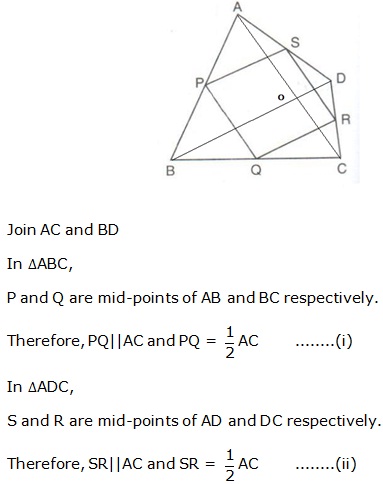
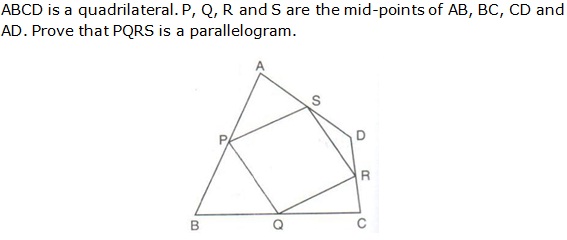
Question 7

Solution 7

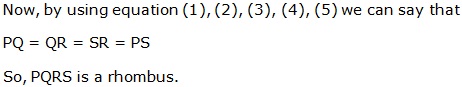
Question 8

Solution 8

Question 9

Solution 9

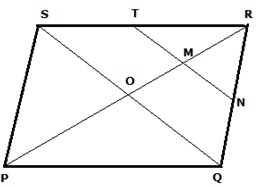
Question 10

Solution 10

Question 11

Solution 11

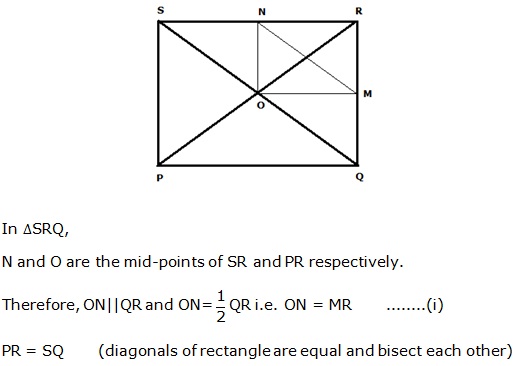
Question 12

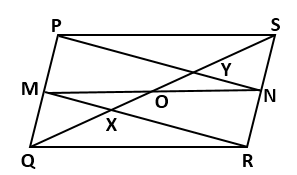
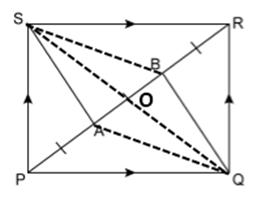
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that

RN and RM trisect QS.

Solution 12

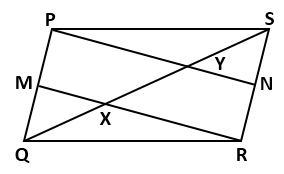
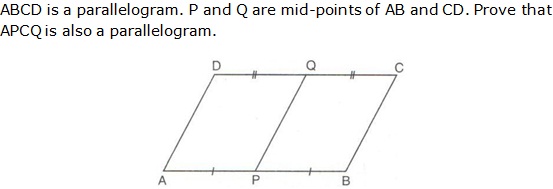
Question 13

In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that

PMRN is a parallelogram.

Solution 13

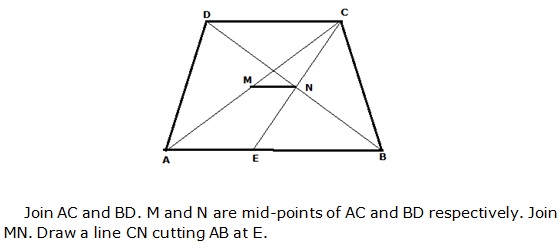
Question 14

In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that

MN bisects QS.

Solution 14

Question 15

Solution 15

Question 16

Solution 16

Question 17

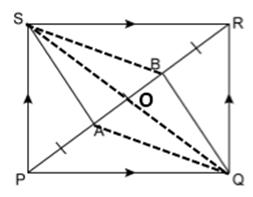
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that:

SA ‖ QB and SA = QB.

Solution 17

Construction:

Join BS and AQ.

Join diagonal QS.

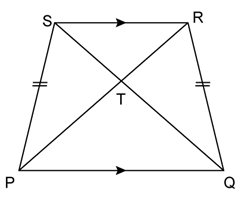
Question 18

In the given figure, PQRS is a parallelogram in which PA = AB = Prove that:

SAQB is a parallelogram.

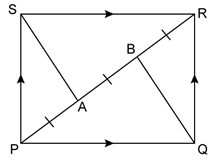
Solution 18

Construction:

Join BS and AQ.

Join diagonal QS.

Question 19

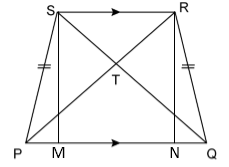
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that:

∠PSR = ∠QRS and ∠SPQ = ∠RQP

Solution 19

Construction:

Draw SM ⊥ PQ and RN ⊥ PQ

Question 20

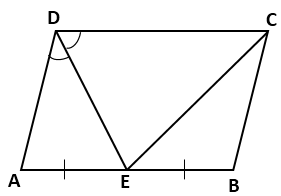
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:

1. BC = BE.
2. CE is the bisector of angle C and angle DEC is a right angle

Solution 20

Question 21

Prove that if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.

Solution 21

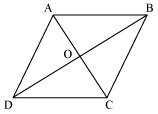
Let ABCD be a quadrilateral, whose diagonals AC and BD bisect each other at right angle.

i.e. OA = OC, OB = OD

And, ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°

To prove ABCD a rhombus, we need to prove ABCD is a parallelogram and all sides of ABCD are equal.

Now, in ΔAOD and DCOD

OA = OC  (Diagonal bisects each other)

∠AOD = ∠COD (Each 90°)

OD = OD   (common)

∴ΔAOD ≅ΔCOD  (By SAS congruence rule)

∴ AD = CD  ….(i)

Similarly, we can prove that

AD = AB and CD = BC ….(ii)

From equations (i) and (ii), we can say that

AB = BC = CD = AD

Since opposite sides of quadrilateral ABCD are equal, so, we can say that ABCD is a parallelogram.

Since all sides of a parallelogram ABCD are equal, so, we can say that ABCD is a rhombus.

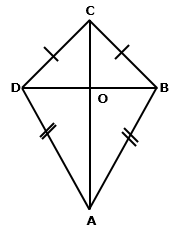
Question 22

Prove that the diagonals of a kite intersect each other at right angles.

Solution 22

Consider ABCD is a kite.

Then, AB = AD and BC = DC

Question 23

Prove that the diagonals of a square are equal and perpendicular to each other.

Solution 23