FRANK Solutions for Class 9 Physics Chapter 4 - Fluids

FRANK Solutions for Class 9 Physics Chapter 4 - Fluids

Chapter 4 - Fluids Exercise 157

Question 1

What do you mean by pressure? Write its SI unit.

Solution 1

The thrust on the unit surface is known as pressure. The SI unit of pressure is Nm^-2.

Question 2

What is the difference between thrust and pressure?

Solution 2

Thrust on a surface is the force acting normally on a surface while pressure on a surface is thrust acting on the unit area of a surface.

Question 3

(i) Calculate the height of a water column which will exert on its base the same
Pressure as the 70 cm column of mercury.
(ii) Will the height of the water column change if the cross section of the water column is made wider?

Solution 3

Question 4

Explain, why a gas bubble released at the bottom of a lake grows in size as it rises to the surface of the lake.

Solution 4

Lake has greater pressure at the bottom than the surface as pressure increases with depth. So when gas bubble is released at the bottom of the lake it experiences more pressure and is small in size but as it rises upwards the pressure experienced by it decreases. So it grows in size as it moves towards the surface from bottom.

Question 5

A dam has broader walls at the bottom than at the top. Explain.

Solution 5

A dam has broader walls at the bottom than at the top because the pressure exerted by a liquid increases with its depth, and at any point at a particular depth liquid pressure is same in all directions. Now as more pressure is exerted by water on the wall of the dam as depth increases. Hence a thick wall is constructed at the bottom of dam to withstand greater pressure.

Question 6

The base of a cylindrical vessel measures 300 cm². Water (density = 1000 kg m^-3) is poured into it upto a depth of 6 cm. Calculate the pressure and thrust of water on the base. (g = 10 m s^-2)

Solution 6

Question 7

State three factors on which the pressure at a point in a liquid depends.

Solution 7

The pressure at a point in a liquid depends upon on the following three factors:
(i) It depends on the point below the free surface (h).
(ii) It depends on density of liquid (p).
(iii) It depends upon acceleration due to gravity (g) of the place.

Question 8

Deduce an expression for the pressure at a depth inside the liquid.

Solution 8

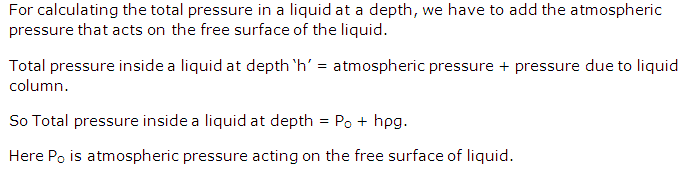
Question 9

What is meant by a fluid? What is a fluid pressure?

Solution 9

A substance having a tendency to flow is called fluid.
A fluid exerts pressure on the bottom due to its weight and on the walls of the container in which it is enclosed by virtue of its ability to flow. This is called fluid pressure.

Question 10

State the laws of liquid pressure.

Solution 10

The laws of liquid pressure are
(i) Pressure inside the liquid increases with the depth from the free surface of the liquid.
(ii) Pressure is same at all points on a horizontal plane, in case of a stationary liquid.
(iii) Pressure is same in all directions about a point inside the liquid.
(iv) Pressure at same depth is different in different liquids. It increases with the increase in the density of the liquid.
(v) A liquid will always seek its own level.

Question 11

How does the liquid pressure on a diver change according to the following conditions:
(i) When the driver moves horizontally, and
(ii) When the driver moves to the greater depth?

Solution 11

Question 12

The atmospheric pressure is 75 cm of mercury. Express it in Nm^-2.

Solution 12

Pressure is given by
P = h Xp Xg.
Where h is height of liquid column, p is density of liquid, g is acceleration due to gravity.
Density of mercury is = 1.36 X10⁴ kg/m³.
h= height of mercury column which is given = 75 cm = 0.75 m.
So pressure = 0.75 X 1.36 X10⁴X9.8 = 9.996X104Nm^-2.

Question 13

What do you mean by diver's suit?

Solution 13

A diving suit is a garment or device designed to protect a diver from the underwater environment.

Question 14

Name some ambient pressure diving suits.

Solution 14

There are five main types of ambient pressure suits. These are wetsuits, drysuits, semidry suits, dive skins etc.

Question 15

Solution 15

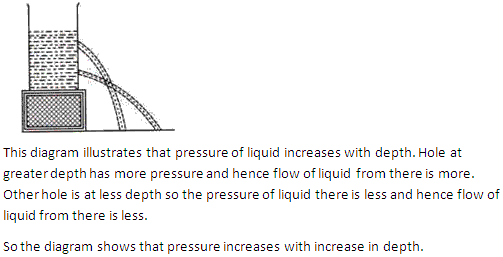
Question 16

What is a manometer? How does it show whether the pressure inside a vessel connected to one arm of it, is lower or above the atmospheric pressure?

Solution 16

Manometer is a simple pressure gauge that measures differences in pressure at the two ends of the apparatus.
Manometer is a U shaped tube containing water whose one limb is dipped in vessel and vessel is tightly covered with plastic sheet. U shaped tube has two limbs one towards the vessel and other is opened to atmosphere.
Now if level of water toward atmospheric open limb is more than level of water in limb towards apparatus end then liquid is said to be at higher pressure than atmosphere. And if level of water toward atmospheric open limb is less than level of water in limb towards apparatus end then liquid is said to be at lower pressure than atmospheric pressure.

Question 17

Is pressure a scalar or vector physical quantity?

Solution 17

Pressure is a scalar physical quantity.

Question 18

Define one Pascal.

Solution 18

One pascal is defined as the pressure exerted on a surface of area 1 m² by a force of 1 Newton acting normally on the surface.

Question 19

What do you mean by thrust? Write its SI unit.

Solution 19

The force acting normally on a surface is known as thrust.
SI unit of thrust is N.

Question 20

What length of water column is equivalent to 0.76 m mercury column?

Solution 20

Question 21

Why can't water be used in place of mercury in a barometer?

Solution 21

Water can't be used in place of mercury in a barometer because of its low density. It would require 10.34 m long tube to measure 1 atmospheric pressure which is not practically possible while mercury having high density (13.6 g/cc) would require only 0.76 m long pipe which is practically possible.

Question 22

What physical quantity is measured in bar?

Solution 22

Pressure is the physical quantity which is measured in bar.

Question 23

State whether thrust is scalar or vector.

Solution 23

Thrust is a vector quantity.

Chapter 4 - Fluids Exercise 158

Question 1

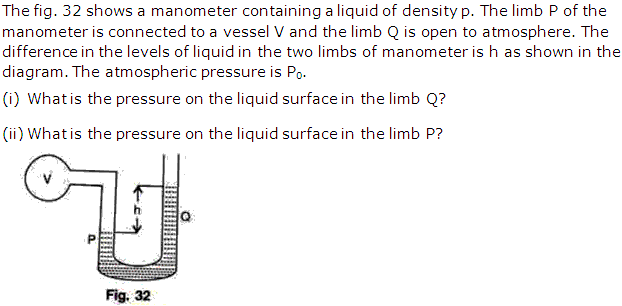
Solution 1

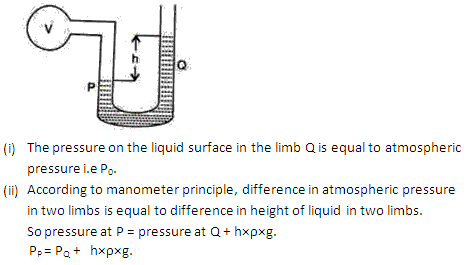
Question 2

State the principle on which a hydraulic press works. Write one use of hydraulic press.

Solution 2

A hydraulic press works on the principle of pascal's law. A hydraulic press can be used for extracting juice of sugarcane, sugar beet etc.

Question 3

State Pascal's law of transmission of pressure. Name three applications of Pascal's law.

Solution 3

Pascal's law states that pressure applied to an enclosed liquid, is transmitted equally to every part of the liquid or in other words when pressure is applied at a point in a confined fluid, it is transmitted undiminished and equally in all directions throughout the liquid.
Hydraulic machines such as hydraulic press, hydraulic brakes and hydraulic jack are application of pascal's law.

Question 4

What is the use of altimeter?

Solution 4

Altimeter is a device which is used in an aircraft to measure its altitude.

Question 5

How does atmosphere pressure very with height?

Solution 5

Atmospheric pressure decreases with increase in height. our atmosphere comprises of a large number of parallel layers. The pressure on a layer is equal to the thrust or weight of the gaseous column on the unit area of that layer. Hence, as we go up, the weight of the gaseous column decreases, which decrease the pressure of the gaseous column.

Question 6

Why is aneroid barometer called so?

Solution 6

Aneroid means containing no liquid and aneroid barometer is evacuated so it tends to collapse under the pressure of air. The stout spring balances the thrust on the metal box due to normal air pressure and prevents the box from collapsing. As this type of barometer doesn't contain any liquid so it got its name aneroid barometer.

Question 7

What is a barometer write two uses of a barometer?

Solution 7

Barometer is a device which is used for measuring atmospheric pressure. Barometers are used in weather forecasting and in measuring altitudes.

Question 8

Why is mercury used in a barometer?

Solution 8

Mercury is used in barometer because
(i) It can be obtained in pure form.
(ii) It does not vaporizeat ordinary temperatures.
(iii) Its density is high and hence the length of the mercury column supported by atmospheric pressure is 76 cm which is practically possible.

Chapter 4 - Fluids Exercise 173

Question 1

What is meant by the term buoyancy?

Solution 1

All liquid exerts an upward force on the body placed in it. This Phenomenon is called buoyancy.

Question 2

A body weighs 300 gf in air and 280 gf when completely immersed in water. Calculate:
(i) The loss in weight of the body,
(ii) The upthrust on the body.

Solution 2

Weight of the body in air = 300 gf.
Apparent Weight of the completely immersed body in water = 280 gf.
(i) Loss in weight of the body = Weight of body in air - apparent weight of immersed body.
Loss in weight = 300 gf - -280 gf = 20 gf.
(ii) As upthrust on the body = loss in weight
(iii) So uptrust = 20 gf.

Question 3

A metal cube of 5 cm edge and density 9 g cm^-3 is suspended by a thread so as to be completely immersed in a liquid of density 1.2 g cm^-3. Find the tension in the thread. (Take g = 10 ms^-2).

Solution 3

Edge of metal cube = 5 cm.
Density of the metal cube = 9 gcm^-3 = 9 X 10³ kgm^-3.
Volume of the metal cube = 125 cm³ = 125X10^-6 m³.
Mass of the metal cube =9 X 10³X125X10^-6 = 1125 X10^-3 =1.125 kg.
Weight of the liquid = mass X gravity = 1.125 X10 = 11.25 N.
Density of liquid = 1.2 gcm^-3= 1.2 X10³ kgm^-3.
Upthrust of the liquid = V X p Xg.
Upthrust = 125X10-6 X1.2 X103 X10 = 1.5 N.
Apparent weight of the body = weight of liquid - upthrust
Apparent weight = 11.25 N - 1.5 N = 9.75 N
Tension in the string is equal to the apparent weight of the body
So, tension in string would be 9.75 N.

Question 4

It is easier to lift a heavy stone under water than in air. Explain.

Solution 4

It is easier to lift a heavy stone under water because in water an upthrust acts on the upward direction which reduces the apparent weight of the stone and makes it easy to lift.

Question 5

State Archimedes' principle.

Solution 5

Principle of Archimedes' states that when a body is totally or partially immersed in a fluid, it experiences an upthrust equal to the weight of the fluid displaced by it.

Question 6

Describe an experiment to verify the Archimedes' principle.

Solution 6

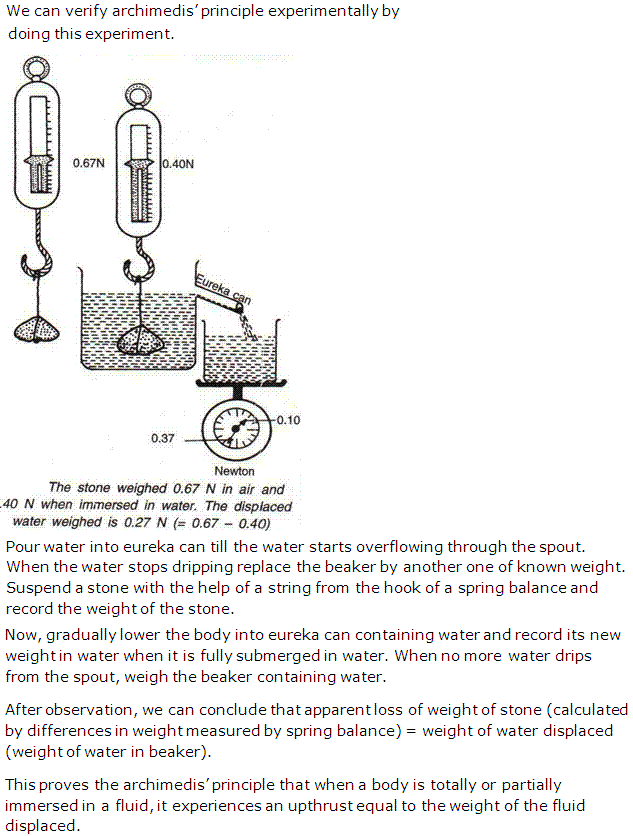
Question 7

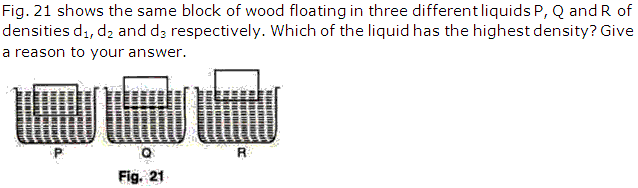
Solution 7

Question 8

Define up thrust and state its SI unit.

Solution 8

The upward force which any liquid exerts upon a body placed in it is called the upthrust. The SI unit of upthrust is N.

Question 9

In what direction does the buoyant force act on a body due to a liquid?

Solution 9

Buoyant force act on a body in upward direction.

Question 10

What do you mean by the term upthrust of a liquid?

Solution 10

Upthrust is defined as the upward force on the object provided by the liquid because the object has displaced some of the fluid.

Question 11

Why is a force needed to keep a block of cork inside water?

Solution 11

When block of cork is immersed in water buoyant force acts on it in upward direction so to overcome this force we have to apply an equal force in downward direction to keep block of cork inside water.

Question 12

A piece of wood when left under water again comes to the surface. Explain with reason.

Solution 12

Wood has density less than water so volume of water displaced by it is more than the volume of wooden block submerged so force of upthrust is greater than the weight of wood which pushes wooden block on the surface. Hence, a piece of wood when left under water again comes to the surface.

Question 13

Will a body weigh more in air or in water when weighed with a spring balance? Why?

Solution 13

A body will weigh more in air as weight of body acts in downward direction and there is no force in upward direction while body submerged in water weigh less because an upthrust act on the body in upward direction so the resultant weight of the body decreases.

Question 14

A body dipped into a liquid experiences an upthrust. State two factors on which upthrust on the body depend.

Solution 14

Upthrust or buoyant force depends on the following factors:
(i) Volume of body submerged in the liquid.
(ii) Density of the liquid.
(iii) Acceleration due to gravity.

Question 15

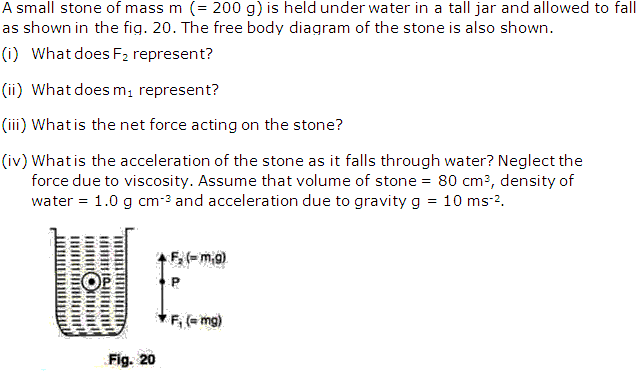
Solution 15

Chapter 4 - Fluids Exercise 174

Question 1

When a piece of wood is suspended from the hook of a spring balance, it reads 90 gf. The wood is now lowered into water. What reading do you expect on the scale of the spring balance?

Solution 1

Wood has density less than water so volume of water displaced by it is more than the volume of wooden block submerged so force of upthrust is greater than the weight of wood which makes it float on the water surface. And the apparent weight of the piece of the wood would be zero.

Question 2

An iron ball of mass 600 g is dropped in mercury contained in a beaker. Will the ball float or sink? What will be its apparent weight?

Solution 2

Density of iron is less than the density of mercury so it will float on the surface of the mercury. Apparent weight of the floating iron ball is zero.

Question 3

Explain, why an iron nail floats on mercury, but it sinks in water.

Solution 3

Iron nail has density less than that of mercury so it will float on the surface of mercury but in the case of water it will sink because the density of iron nail is more than that of water.

Question 4

Is density of a body same as its relative density?

Solution 4

No, the relative density of a substance is the ratio of the density of the substance to the density of water at 4^oC.

Question 5

Write the SI units of
(i) Buoyant force
(ii) Density
(iii) Weight of a body
(iv) Relative density

Solution 5

(i) SI unit of buoyant force is N.
(ii) SI unit of density is Kgm^-3.
(iii) SI unit of weight of body is N.
(iv) Relative density is a pure ratio it has no dimension.

Question 6

An iron nail sinks in water while an iron ship floats on water. Explain the reason.
What can you say about the average density of a ship floating on water?

Solution 6

Density of iron is more than the density of water so it sinks down in the water but in case of ship, it is design in such a manner that it encloses large quantity of air in air tight bags and in rooms and corridors which makes the average density of ship less than that of water and ship floats on the surface of the water.

Question 7

A piece of ice floating in a glass of water melts but level of water in the glass does not change. Give reason.

Solution 7

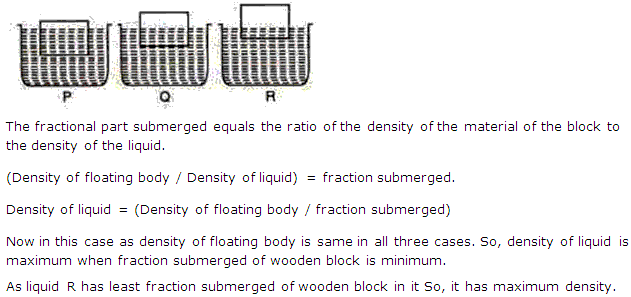
The fractional part submerged equals the ratio of the density of the material of the block to the density of the liquid.
(Density of floating body / Density of liquid) = fraction submerged.
The Fraction of ice submerged in water remain same as density of ice and water remain same during melting. As ice melts some volume of ice decrease and convert into water and volume of water increase by same amount. So, level of water remains same during melting.

Question 8

A piece of wood of uniform cross-section and 15 cm height sinks 10 cm in water and 12 cm in spirit. Find the R.D. of wood and spirit.

Solution 8

The fractional part submerged equals the ratio of the density of the material of the block to the density of the liquid.
(Density of floating body / Density of liquid) = fraction submerged.
Height of wooden piece = 15 cm.
Height of wooden piece sinks in water = 10 cm.
Fraction of wooden piece submerged in water = 10/15 = 0.67.
As liquid is water so ratio of Density of wooden by density of water gives relative density of floating wooden piece. So, relative density of wooden block is 0.67.
 Height of wooden piece = 15 cm.
Height of wooden piece sinks in spirit = 12 cm.
Fraction of wooden piece submerged in water = 12/15 = 0.8.
We know density of wooden piece = 0.67
(Density of floating body / Density of liquid) = fraction submerged.
Density of liquid/spirit = (Density of floating body /fraction submerged)
Density of liquid/spirit = 0.67/0.8 = 0.83.
Relative density of spirit is 0.83.

Question 9

A man first swims in sea water and then in river water.
(i) Compare the weight of sea water and the river water displaced by him.
(ii) Where does he find it easier to swim and why?

Solution 9

(i) When a body is completely immersed in water then it displaces equal volume of water to its own weight. Volume of body of man is same in both river and sea so weight of water of sea displaced by him is equal to the weight of water of river displaced by him. And ratio of weights would be 1:1.
(ii) Sea water contains mineral salts and density of sea water increase due to presence of these. As density of sea water is more than the normal water so it apply more buoyant force than usual one and a person find it easy to swim in sea water.

Question 10

The R.D. of ice is 0.92 and that of sea water is 1.025. Find the total volume of an iceberg which floats with its volume 800 cm³ above water.

Solution 10

Relative density of Ice = 0.92
Relative density of sea water = 1.025
Let total volume of iceberg = X cm³.
Volume of iceberg above water = 800 cm³.
Volume of iceberg in submerged in the water = (X - 800) cm³.
Fraction of iceberg submerged = (X- 800)/X
Now we know that fractional part submerged equals the ratio of the density of the material of the block to the density of the liquid.
(Density of ice / Density of sea water) = fraction submerged
0.92/1.025 = (X-800)/X
0.8975 X = X - 800
X - 0.8975 X = 800
0.1025 X = 800
X = 800/0.1025 = 7804.8 cm³.
Total volume of iceberg = 7804.8 cm³.

Question 11

A piece of wax floats in brine. What fraction of its volume will be immersed?
R.D. of wax = 0.95, R.D. of brine = 1.1.

Solution 11

Relative density of wax = 0.95
Relative density of brine = 1.1
(Density of wax/ Density of brine) = fraction submerged
0.95/1.1 = fraction of volume submerged
Fraction of volume submerged = 0.86

Question 12

If the density of ice is 0.9 g cm, what portion of an iceberg will remain below the surface of water in the sea? (Density of sea water= 1.1 g cm^-3)

Solution 12

Relative density of Ice = 0.9 cm
Relative density of sea water = 1.1 cm
(Density of ice / Density of sea water) = fraction submerged of iceberg
0.9/1.1 = fraction of iceberg submerged
Fraction of iceberg submerged = 9/11.

Question 13

What is the common use of a lactometer?

Solution 13

Lactometer is commonly used for testing the purity of milk.

Question 14

What is the density of water at 4⁰C in SI system?

Solution 14

Density of water at 4^oc in SI system is = 1000 Kgm^-3.

Question 15

A wooden cube of side 10 cm has mass 700 g. It will float in water with:
(a) Half of its volume inside water
(b) 3 cm height above the water surface
(c) 7 cm height above the water surface
(d) Just inside the water surface.

Solution 15

Side of wooden cube = 10 cm.
Volume of wooden cube = 10 X 10 X 10 = 1000 cm³.
Mass of wooden cube = 700 g.
Density of wooden cube = mass/volume = 700/1000 = 0.7 gcm^-3.
Density of water = 1 gcm^-3.
(Density of floating body / Density of liquid) = fraction submerged
0.7/1 =fraction submerged
Fraction of wooden cube submerged in water = 0.7
Height of wooden cube = 10 cm
Part of wooden cube which is submerged = 10 X 0.7 = 7 cm
So, wooden cube will float in water with 3 cm height above the water surface.

Question 16

A block of wood of mass 24 kg floats in water. The volume of the wood is 0.032 m³. Find:
(a) The volume of the block below the surface of water.
(b) The density of the wood.
(Density of water = 1000 kg m^-3)

Solution 16

Volume of wooden block = 0.032 m³.
Mass of wooden block = 24 Kg.
Density of wooden block = mass/volume = 24/0.032 = 750 Kgm^-3.
Density of water = 1000 Kgm^-3.
(Density of floating body / Density of liquid) = fraction submerged
750/1000 =fraction submerged
Fraction of wooden block submerged in water = 0.75
Total volume of wooden block = 0.032 m³.
Part of volume of wooden block which is submerged = 0.032 X 0.75 = 0.024 m³.

Question 17

If R.D. of platinum is 21.50, what does it signify?

Solution 17

Relative density = density of substance /density of water at 4⁰C.
As relative density of platinum is 21.50, this means platinum is 21.5 times denser than water at 4^oC.

Chapter - Exercise

Solution 1

Chapter 4 - Fluids Exercise 175

Question 1

Density of mercury is 13600 kg m^-3. What is its relative density?

Solution 1

Density of mercury = 13600 Kgm^-3.
Density of water at 4^oC = 1000 kg m^-3.
Relative density = density of substance /density of water at 4⁰C.
Relative density of mercury = 13600 Kgm^-3/1000 kg m^-3 = 13.6.

Question 2

A body of volume 100 cm³ weighs 1 kgf in air. Find its weight in water and its relative density.

Solution 2

volume of body = 100 cm³.
Weight of body = 1 kgf = 1000 gf
Mass of body= 1000 gm.
Density of liquid = 1000 gm/100cm³ = 10 gcm³.
Density of water at 4^o = 1gcm^-3.
Relative density = density of substance /density of water at 4⁰ C
Relative density = 10 gcm³ /1 gcm³ = 10
Mass of body= 1000 gm.
Density of water = 1 gcm^-3
Acceleration due to gravity = 10 ms^-2.
Upthrust = V X p Xg.
Upthrust = 100 X 1 Xf = 100 gf.
Resultant weight of the body = weight - upthrust = 1000 gf - 100 gf = 900 gf.

Question 3

A body of mass 70 kg, when completely immersed in water, displaces 20,000 cm³ of water. Find the relative density of material of the body.

Solution 3

When a body is completely immersed in water then it displaces equal volume of water to its own weight.
So, volume of body = 20000 cm³.
 Mass of body = 70 kg = 70000 gm
Density of body = mass /volume = 70000/20000= 3.5 gm cm^-3.
Density of water in C.G.S system = 1g cm^-3.
Relative density of body = density of body /density of water =3.5 gm cm^-3/1g cm^-3.
Relative density = 3.5.

Question 4

The relative density of mercury is 13.6. State its density in
(i) C.G.S. unit,
(ii) S.I. unit.

Solution 4

Relative density = density of mercury /density of water.
Density of mercury = relative density X density of water.
Relative density = 13.6.
Density of water in C.G.S system = 1g cm^-3.
So, density of mercury in C.G.S system = 13.6 X1 = 13.6 gcm^-3.
Density of water in SI system = 1000 Kg m^-3.
So, density of mercury in SI system = 13.6 X1000 = 13.6 X10³ Kgcm^-3.

Question 5

Solution 5

Density of iron is = 7.8 X 10³ Kg m^-3.
Density of water at 4^oC = 10³ Kg m^-3.
Relative density of a substance is the ratio of the density of the substance to the density of water at 4^oC.
So, relative density of iron is = 7.8 X 10³ Kg m^-3/10³ Kg m^-3 = 7.8

Question 6

How is
(i) mass,
(ii) volume, and
(iii) Density of a metallic piece affected, if at all, with increase in temperature?

Solution 6

(i) Mass of a metallic piece remains unchanged with increase in temperature.
(ii) Volume of metallic piece increases with increase in temperature.
(iii) Density of metallic piece decreases with increases in temperature.

Question 7

How does the density of water change with temperature?

Solution 7

Density of water decreases with the increase in temperature and increases with decreases in temperature.

Question 8

Solution 8

Chapter 4 - Fluids Exercise 177

Question 1

What do you mean by buoyancy?

Solution 1

All liquid exerts a upward force on the body placed in it. This Phenomenon is called buoyancy.

Question 2

State Pascal's law.

Solution 2

Pascal's law states that pressure applied to an enclosed liquid, is transmitted equally to every part of the liquid or in other words when pressure is applied at a point in a confined fluid, it is transmitted undiminished and equally in all directions throughout the liquid.

Question 3

Do all liquids exert pressure?

Solution 3

Yes, all liquid exert pressure.

Question 4

State two applications of Pascal's law.

Solution 4

Hydraulic machines such as hydraulic press, hydraulic brakes and hydraulic jack are application of pascal's law.

Question 5

What is the principle of a hydraulic machine?

Solution 5

Pascal's law is principle of hydraulic machines.

Question 6

State the principle on which Brahma press depends.

Solution 6

Brahma press depends upon Pascal's law.

Question 7

State two uses of a hydraulic press.

Solution 7

(i) A hydraulic press can be used for extracting juice of sugarcane, sugar beet etc.
(ii) A hydraulic press can be used for pressing cotton bales, quilts, books etc.

Question 8

What is meant by atmospheric pressure?

Solution 8

Atmospheric point at any point in air at rest is equal to the weight of a vertical column of air on a unit area surrounding the point, the column extending to the top of atmosphere.

Question 9

What is the value of atmospheric pressure?

Solution 9

Atmospheric pressure at sea level is about 10⁵ N/m².

Question 10

Name the instrument used to measure atmospheric pressure.

Solution 10

Barometer is used for measuring the atmospheric pressure.

Question 11

What is the use of altimeter?

Solution 11

Altimeter is a device which is used in an aircraft to measure its altitude.

Question 12

What is meant by up thrust?

Solution 12

The upward force which any liquid exerts upon a body placed in it is called the upthrust.

Question 13

What does a falling barometer indicate?

Solution 13

A falling barometer indicates the approach of rain or storm or both.

Question 14

Is pressure a vector quantity?

Solution 14

Pressure is a scalar quantity.

Question 15

Is thrust a scalar or vector quantity?

Solution 15

Thrust is a vector quantity.

Question 16

What is the SI unit of density?

Solution 16

SI unit of density is Kgm^-3.

Question 17

What do you mean by relative density?

Solution 17

The relative density of a substance is the ratio of the density of the substance to the density of water at 4^oC.

Question 18

What are the factors on which the pressure of a liquid depends?

Solution 18

Question 19

State Archimedes' principle. Does it apply to gases?                   

Solution 19

Principle of Archimedes' states that when a body is totally or partially immersed in a fluid, it experiences an upthrust equal to the weight of the fluid displaced. Yes, it applies to gases also.

Question 20

How is thrust different from pressure?

Solution 20

Thrust on a surface is the force acting normally on a surface while pressure on a surface is thrust acting on the unit area of a surface.

Chapter 4 - Fluids Exercise 178

Question 1

Define atmospheric pressure diving suits. Does a diving suit create buoyancy?

Solution 1

A atmospheric pressure diving suit is a garment or device designed to protect a diver from the underwater environment. Yes, diving suits create buoyancy.

Question 2

What do you mean by the term fluid pressure?

Solution 2

A fluid exerts pressure on the bottom due to its weight and on the walls of the container in which it is enclosed by virtue of its ability to flow. This is called fluid pressure.

Question 3

A dam has broader walls at the bottom than at the top. Explain.

Solution 3

A dam has broader walls at the bottom than at the top because the pressure exerted by a liquid increases with its depth, and at any point at a particular depth liquid pressure is same in all directions. Now as more pressure is exerted by water on the wall of the dam as depth increases. Hence a thick wall is constructed at the bottom of dam to withstand greater pressure.

Question 4

State and explain Pascal's law of transmission of pressure.

Solution 4

Pascal's law states that pressure applied to an enclosed liquid, is transmitted equally to every part of the liquid.
Means when pressure is applied at a point in a confined fluid, it is transmitted undiminished and equally in all directions throughout the liquid.

Question 5

State two factors which affect the atmospheric pressure as we go up.

Solution 5

Factors which affect the atmospheric pressure as we go up are
(i) Weight of gaseous column.
(ii) Density of gaseous column.

Question 6

How does the atmospheric pressure change with altitude?

Solution 6

Atmospheric pressure decreases with increase in height. Our atmosphere comprises of a large number of parallel layers. The pressure on a layer is equal to the thrust or weight of the gaseous column on the unit area of that layer. Hence, as we go up, the weight of the gaseous column decreases, which decrease the pressure of the gaseous column.

Question 7

What is the purpose of a barometer? State two major defects of a simple barometer.

Solution 7

Barometer is a device used for measuring atmospheric pressure.
Simple barometer has two main defects
(i) It is not suitable for making accurate measurement of atmospheric pressure as any change in the level of mercury in the tube changes the level of the free surface of mercury is trough and fixed scale cannot be used with it.
(ii) Simple barometer is not portable. So, it cannot be used by airmen, navigators, mountaineers, who need a portable barometer.

Question 8

Why do not we feel uneasy even under enormous pressure of the atmosphere above as?

Solution 8

We don't feel uneasy even under enormous pressure of the atmosphere above us because our blood also exerts a pressure called blood pressure, which is greater than atmospheric pressure. So, there is balance between our blood pressure and atmospheric pressure.

Question 9

How is the reading of a barometer affected when it is taken to (a) A mine, and (b) A hill?

Solution 9

Reading of a barometer would rise if it is taken to the mine as pressure increases with depth.
Reading of a barometer would fall if it is taken to a hill as pressure decreases with increase in height.

Question 10

A solid weighs 2.10 N in air. It has a relative density of 8.4. How much will the body weigh if placed (i) In water (ii) In a liquid of relative density 1.2?

Solution 10

Weight of solid in air = 2.10 N
Relative density of solid = 8.4
Now, Relative density = weight of solid in air/ loss of weight of solid in water.
Loss of weight of solid in water = weight of solid in air/ Relative density.
Loss of weight of solid in water = 2.10/8.4 = 0.25 N.
Weight of solid in water = weight in air - loss of weight in water
Weight of solid in water = 2.10 - 0.25 =1.85 N.

Relative density of liquid =1.2
We know
Relative density of liquid = Loss of weight of solid in liquid/loss of weight of solid in water.
Loss of weight of solid in liquid = Relative density X loss of weight of solid in water.
Loss of weight of solid in liquid = 1.2 X 0.25 = 0.3 N.
Weight of solid in liquid = weight of solid in air - loss of weight of solid in liquid.
Weight of solid in liquid = 2.10 - 0.3 = 1.8 N.

Question 11

The density of iron is 7800 kg m^-3. What do you mean by this statement? What is density of water at 4⁰C?

Solution 11

Density of iron is 7800Kgm^-3.
This means a cube of iron having side 1m would weigh 7800 Kg.
Density of water at 4^oC is 1000 Kgm^-3.

Question 12

Calculate the mass of a body whose volume is 2m³ and relative density is 0.52.

Solution 12

Relative density of body = 0.52
Density of water at 4^oC = 1000 Kgm^-3.
Density of body = 0.52 X 1000 Kgm^-3= 520 Kgm^-3
We know density = mass X volume.
Mass = density X volume
Mass = 520 X 2 =1040 Kg.
Mass of given body is 1040 Kg.

Question 13

A piece of metal weighs 44.5 gf in air, 39.5 gf in water. What is the R.D. of the metal?

Solution 13

Piece of metal weighs in air = 44.5 f
Piece of metal weighs in liquid = 39.5 f.
Loss of weight of metal in liquid = 44.5 - 39.5 = 5f.
Relative density = weight of solid in air/ loss of weight of solid in water.
Relative density of liquid =44.5f/5f =8.9
Relative density of liquid = 8.9

Question 14

A body of volume 100 cm³ weighs 1 kgf in air. Calculate its weight in water. What is its relative density?

Solution 14

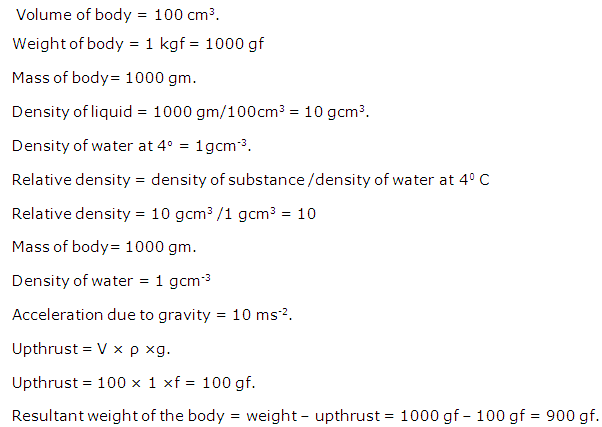
Question 15

State the principle of floatation. What can you say about the average density of a ship floating on water?

Solution 15

Principle of floatation states that a floatating body displaces an amount of fluid equal to its own weight.
Ship is designed in such a manner that it encloses large quantity of air in air tight bags and in rooms and corridors which makes the average density of ship less than that of water.

Question 16

For what purpose is the acid battery hydrometer used?

Solution 16

Acid battery hydrometer is used to check the concentration of sulphuric acid in an acid battery.

Question 17

Explain why an iron nail floats on mercury, but it sinks in water.

Solution 17

Iron nail has density less than that of mercury so it will float on the surface of mercury but in the case of water it will sink because the density of iron nail is more than that of water.

Question 18

State the principle of floatation. Name an instrument based on this principle. State two uses of the instrument that you describe.

Solution 18

Question 19

Explain the following:
(i) A balloon filled with hydrogen rises to a certain height and then stops rising further.
(ii) An egg sinks in fresh water, but floats in a strong solution of salt.
(iii) A hydrometer is made heavy near the bottom.
(iv) Icebergs floating in sea are very dangerous for ships.

Solution 19

(i) A balloon filled with hydrogen has low density than air so it rises over the air but as height increases density of air decreases and at a certain height the density of hydrogen in balloon and density of air become equal. And as there is no density difference there is no pressure difference also and hence balloon stops rising further.
(ii) Density of egg is greater than fresh water so it sinks in fresh water but due to addition of salt density of water increases which makes the density of salt water greater than egg and hence floats in a strong solution of salt.
(iii) The bottom of the hydrometer is made heavier by loading it with lead shots so that it floats vertically with some of its portion outside the surface of water in the jar.
(iv) Relative density of Ice is = 0.9 cm^-3
Relative density of sea water is = 1 cm^-3
(Density of ice / Density of sea water) = fraction submerged of iceberg
0.9/1 = fraction of iceberg submerged
Fraction of iceberg submerged = 9/10.
Thus in colder countries where there are icebergs in oceans, only about 1/10 is seen above water and the remaining water 9/10 remain submerged. Hence, there is danger of these icebergs to the ships sailing in these oceans.

Question 20

Using Archimedes' principle, describe an experiment to find the relative density of a solid which floats on water.

Solution 20

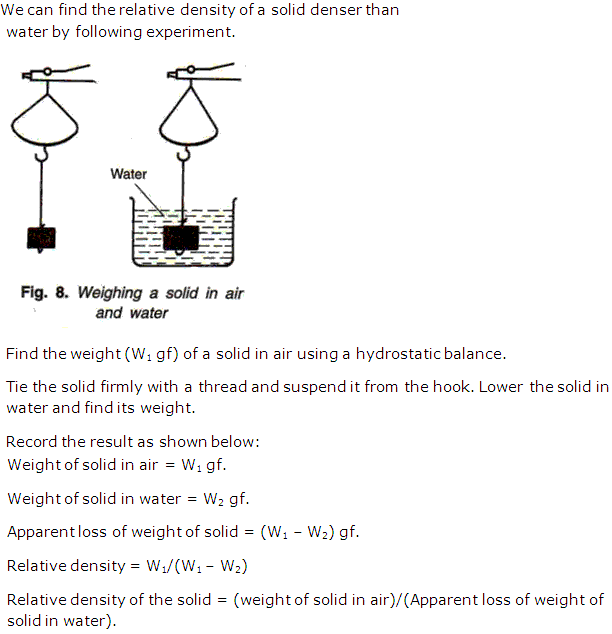
Question 21

Using Archimedes' principle, describe an experiment to find the relative density of a solid denser than water.

Solution 21

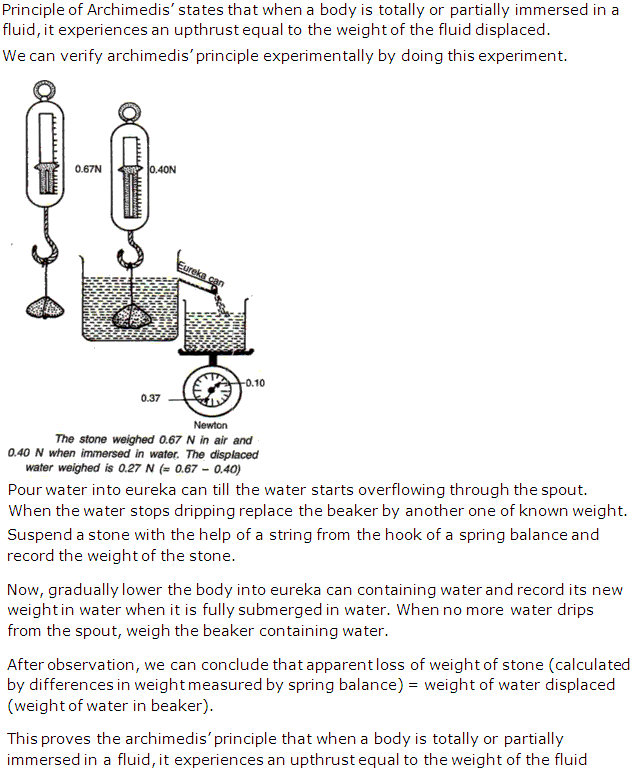
Question 22

State Archimedes' principle, describe an experiment to verify Archimedes' principle.

Solution 22

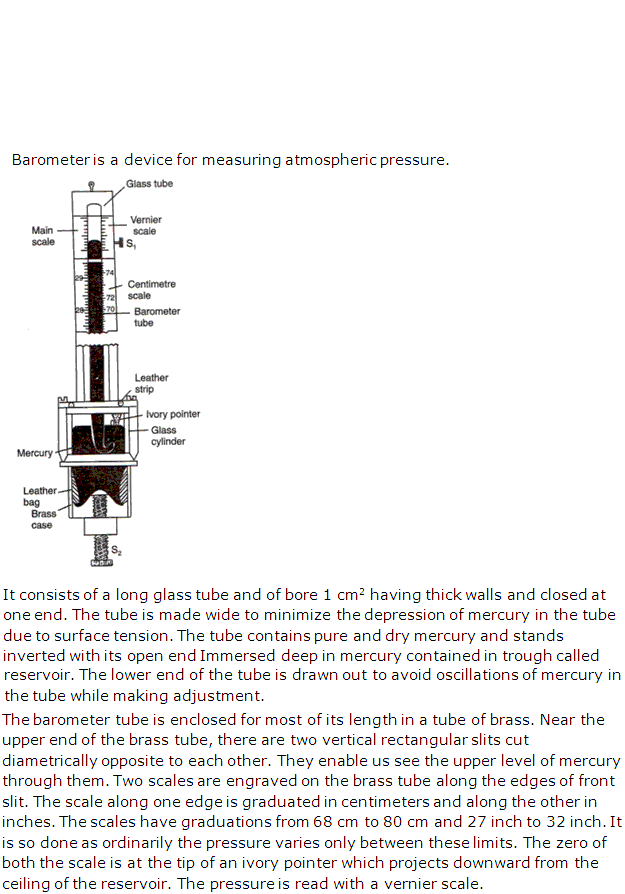
Question 23

What is a barometer? How will you construct a simple barometer?

Solution 23

Question 24

What is an aneroid barometer? Draw a neat and labeled diagram to explain its construction and working.

Solution 24

Question 25

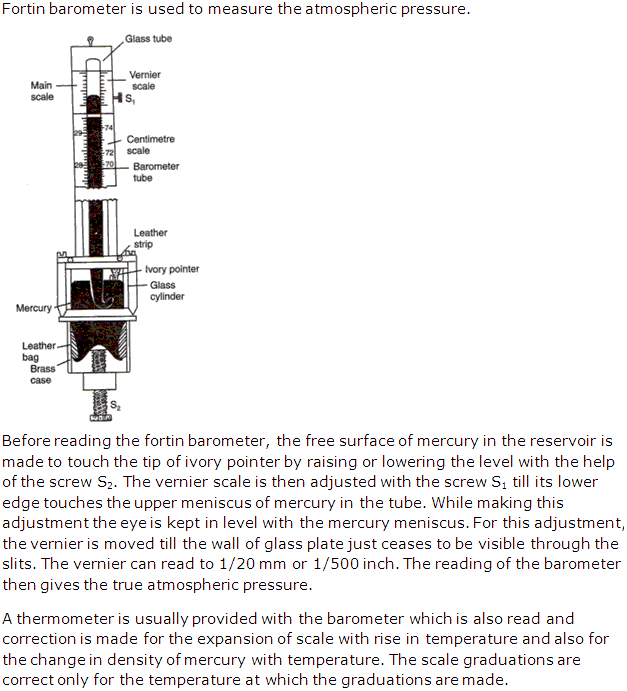
Draw a simple diagram of a Fortin's barometer and state how it is used to measure the atmospheric pressure.

Solution 25

Question 26

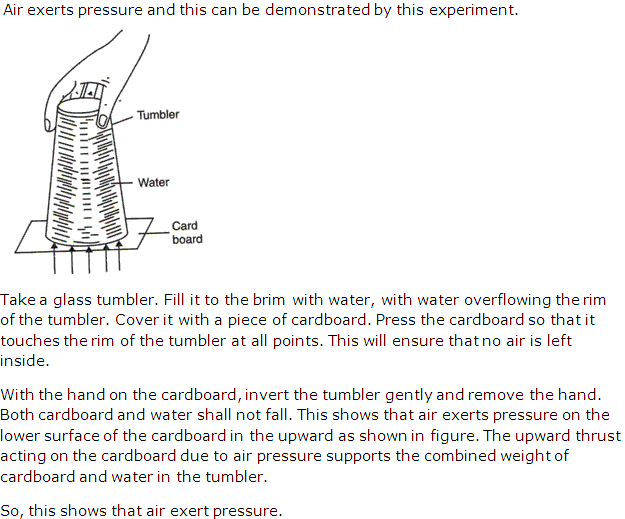
Describe an experiment to demonstrate that air exerts pressure.

Solution 26