FRANK Solutions for Class 9 Maths Chapter 27 - Trigonometrical Ratios of Standard Angles

Chapter 27 - Trigonometrical Ratios of Standard Angles Exercise Ex. 27.1

Question 1

Solution 1

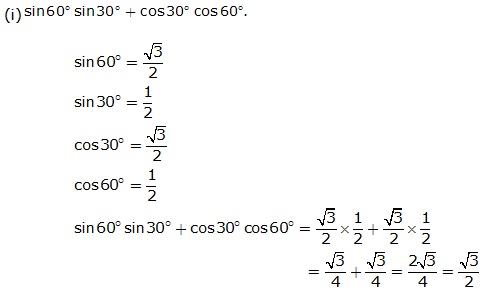
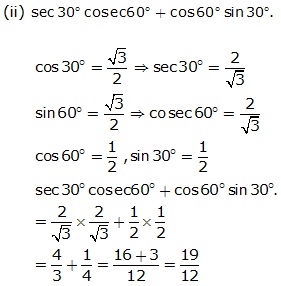
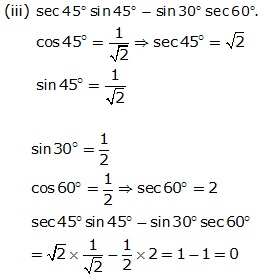
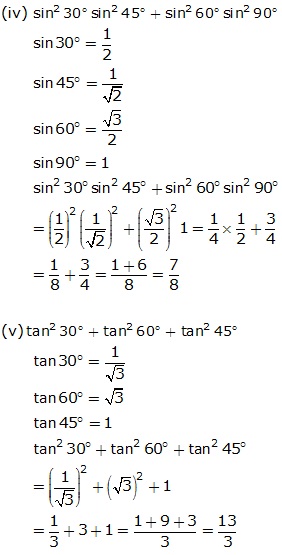
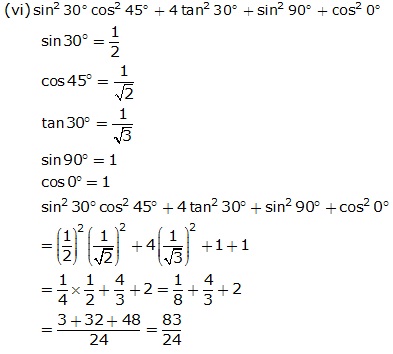
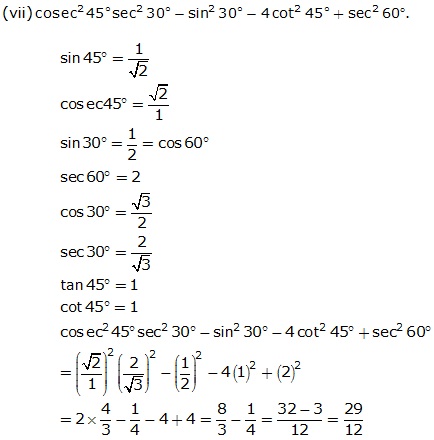
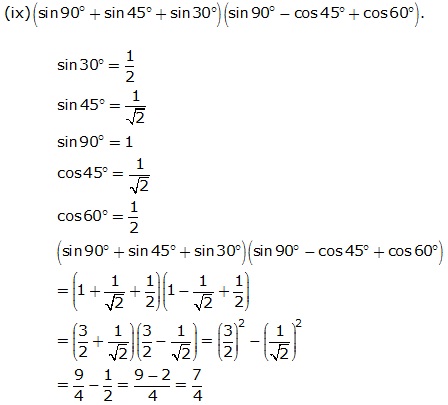
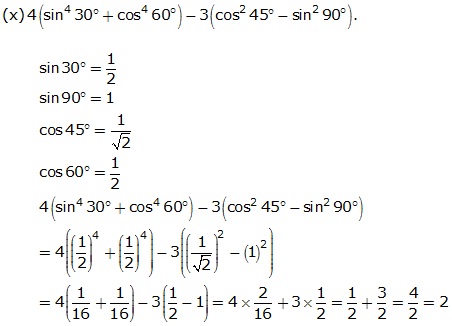
Question 2

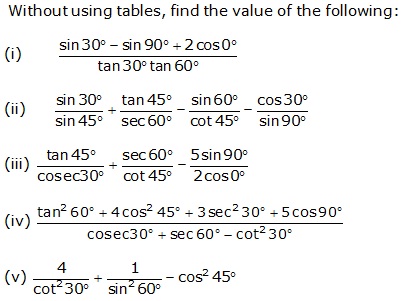
Solution 2

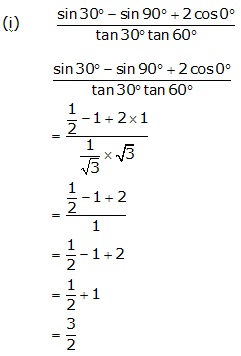
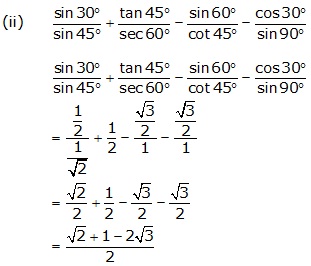
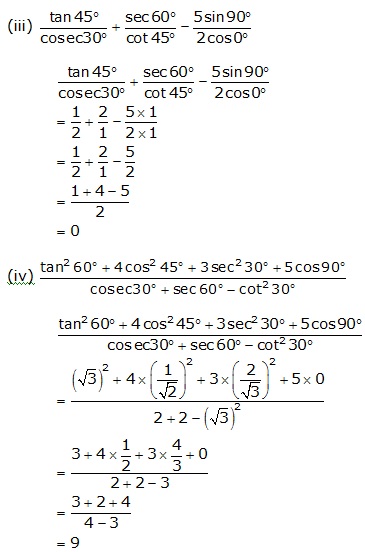
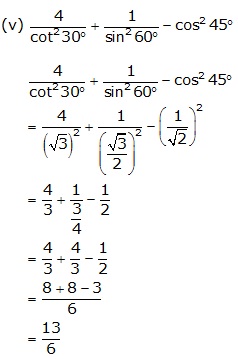
Question 3

Prove that :

sin 60° .cos 30° - sin 60^°. sin 30^° =

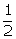
Solution 3

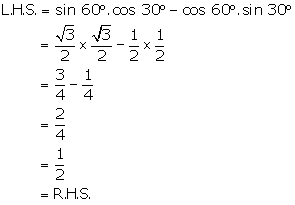
Question 4

Prove that :

cos 60° . cos 30° - sin 60° . sin 30° = 0

Solution 4

Question 5

Prove that :

sec²45° - tan²45° = 1

Solution 5

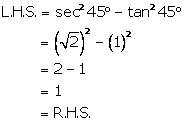
Question 6

Prove that :

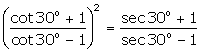
Solution 6

Question 7

Find the value of 'A', if

2 cos A = 1

Solution 7

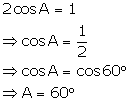
Question 8

Find the value of 'A', if

2 sin 2A = 1

Solution 8

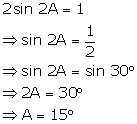
Question 9

Find the value of 'A', if

Solution 9

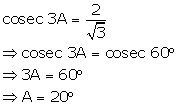
Question 10

Find the value of 'A', if

2 cos 3A = 1

Solution 10

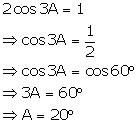
Question 11

Find the value of 'A', if

Solution 11

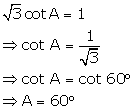
Question 12

Find the value of 'A', if

cot 3A = 1

Solution 12

Question 13

Find the value of 'A', if

(1 - cosec A)(2 - sec A) = 0

Solution 13

Question 14

Find the value of 'A', if

(2 - cosec 2A) cos 3A = 0

Solution 14

Question 15

If sin α + cosβ = 1 and α= 90°, find the value of 'β'.

Solution 15

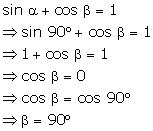
Question 16

Solve for 'Ө':

Solution 16

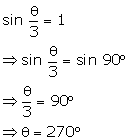
Question 17

Solve for 'Ө':

cot²(Ө - 5)° = 3

Solution 17

Question 18

Solve for 'Ө':

Solution 18

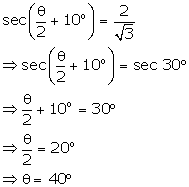
Question 19

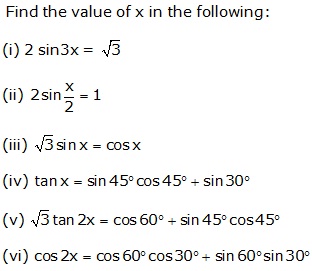
Solution 19

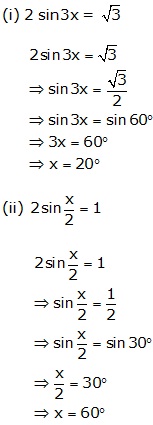
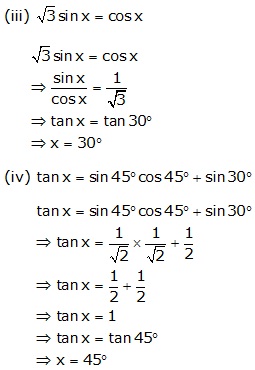
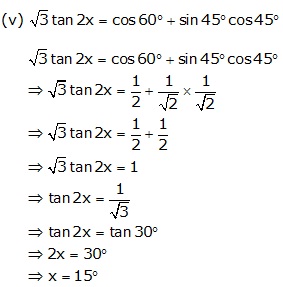
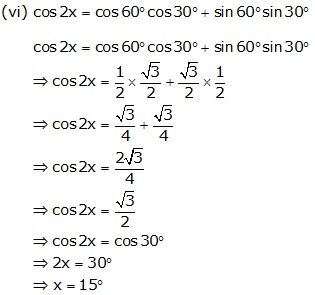
Question 20

If sin Ө = cosӨ and 0° < Ө<90°, find the value of 'Ө'.

Solution 20

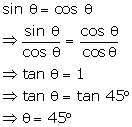
Question 21

If tan Ө= cot Ө and 0°≤Ө≤ 90°, find the value of 'Ө'.

Solution 21

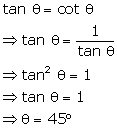
Question 22

Solution 22

Question 23

If Ө = 30°, verify that: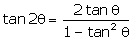

Solution 23

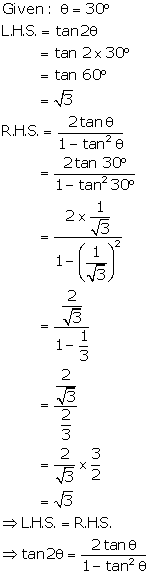
Question 24

If Ө = 30°, verify that: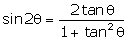

Solution 24

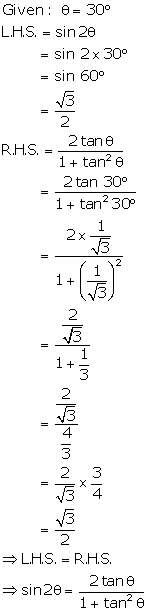
Question 25

If A = 30°, verify that: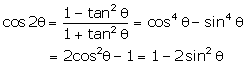

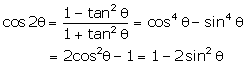
Solution 25

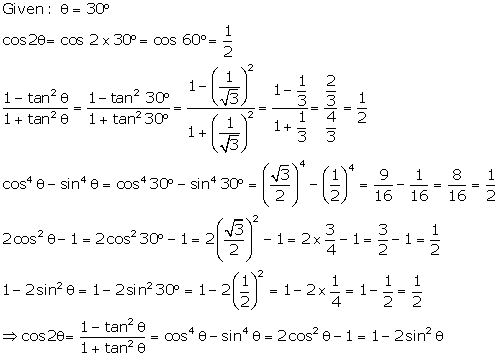
Question 26

If Ө = 30°, verify that:

sin 3Ө = 4sin Ө.sin(60° - Ө) sin(60° + Ө)

Solution 26

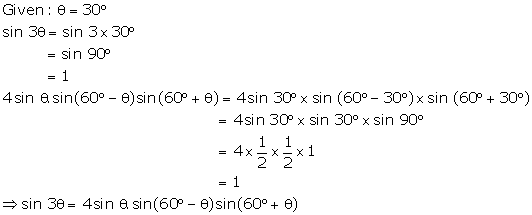
Question 27

If Ө = 30°, verify that:

1 - sin 2Ө= (sin Ө - cosӨ)²

Solution 27

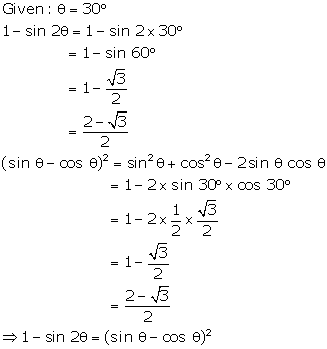
Question 28

Evaluate the following:

Solution 28

Question 29

Evaluate the following:

Solution 29

Question 30

If Ө = 15°, find the value of:

cos 3Ө - sin 6Ө + 3sin (5Ө + 15°) - 2 tan²3Ө

Solution 30

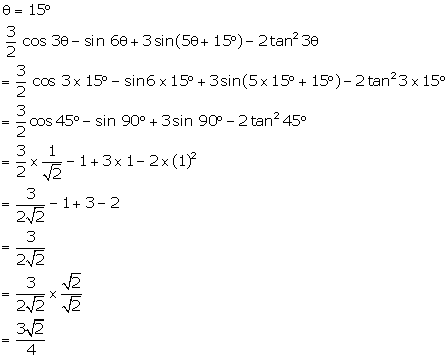
Question 31

If A = 30° and B = 60°, verify that:

sin (A + B) = sin A cos B + cos A sin B

Solution 31

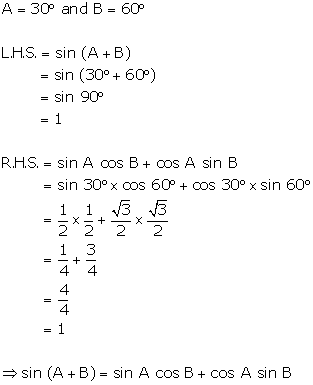
Question 32

If A = 30° and B = 60°, verify that:

cos (A + B) = cos A cos B - sin A sin B

Solution 32

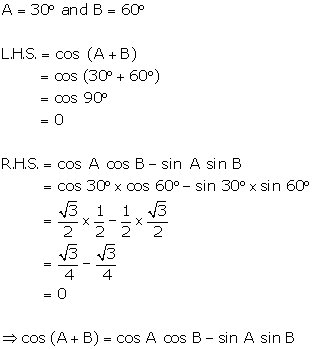
Question 33

If A = 30° and B = 60°, verify that:

Solution 33

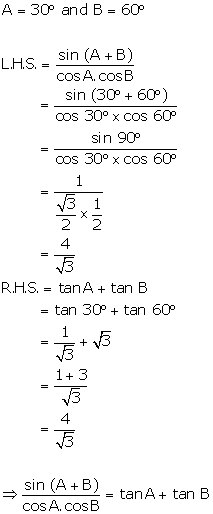
Question 34

If A = 30° and B = 60°, verify that:

Solution 34

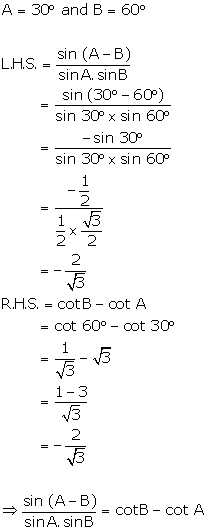
Question 35

If A = B = 45°, verify that

sin (A - B) = sin A .cos B - cos A.sin B

Solution 35

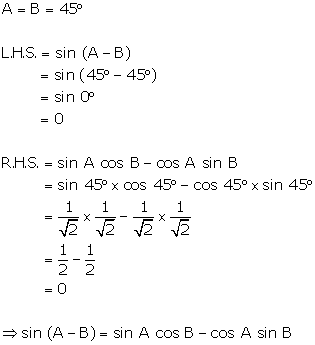
Question 36

If A = B = 45°, verify that

cos (A - B) = cosA.cos B + sin A.sin B

Solution 36

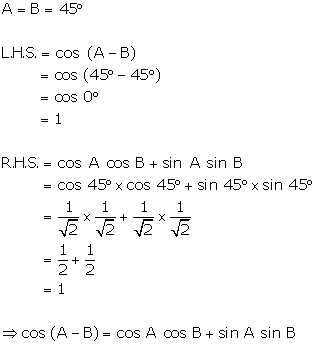
Question 37

Solution 37

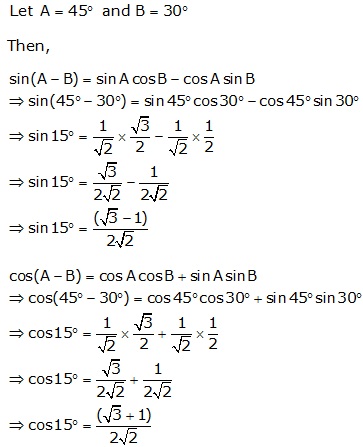
Question 38

If Ө < 90°, find the value of:

sin²Ө + cos²Ө

Solution 38

Question 39

Solution 39

Question 40

If Ө < 90°, find the value of:

Solution 40

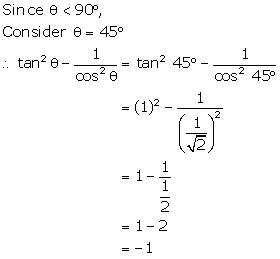
Question 41

Ifsec 2Ө = 2 and Ө< 90°, find the value of

Ө

Solution 41

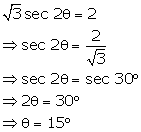
Question 42

Ifsec 2Ө = 2 and Ө< 90°, find the value of

cos 3Ө

Solution 42

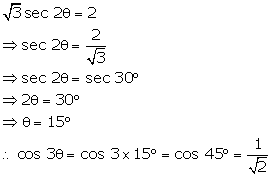
Question 43

Ifsec 2Ө = 2 and Ө< 90°, find the value of

cos² (30° + Ө) + sin² (45° - Ө)

Solution 43

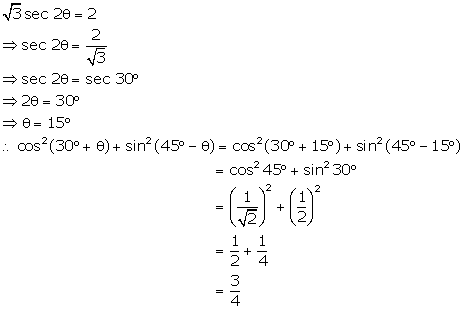
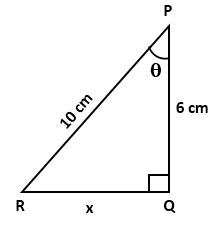
Question 44

In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find

a. cosӨ

b. sin² Ө - cos²Ө

c. Use tan Ө to find the value of RQ

Solution 44

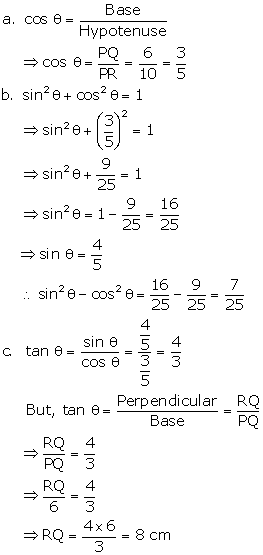
Question 45

Find the value of: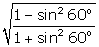

If 3 tan²Ө - 1 = 0, find the value

a. cos 2Ө

b. sin 2Ө

Solution 45

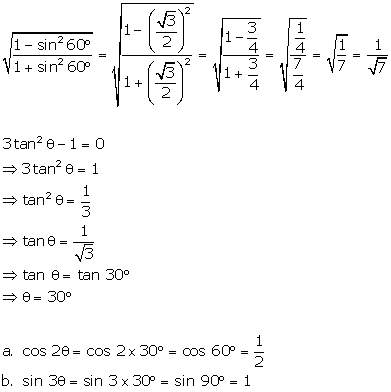
Question 46

Solution 46

Question 47

Solution 47

Question 48

Solution 48

Question 49

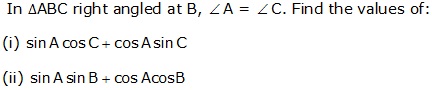
Solution 49

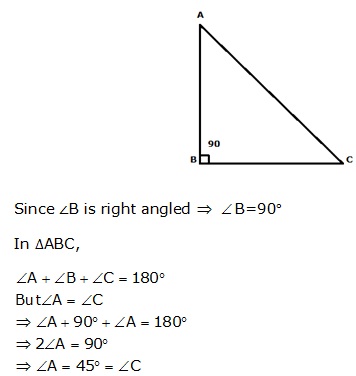
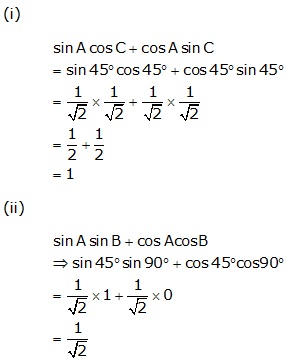
Question 50

Solution 50

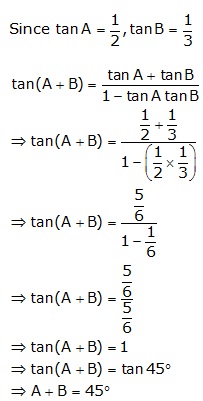
Chapter 27 - Trigonometrical Ratios of Standard Angles Exercise Ex. 27.2

Question 1

Find the value of 'x' in each of the following:

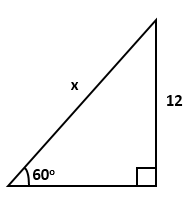
Solution 1

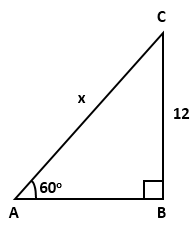
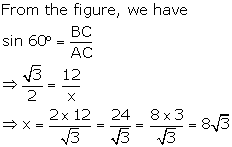
Question 2

Find the value of 'x' in each of the following:

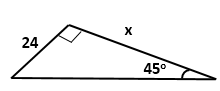
Solution 2

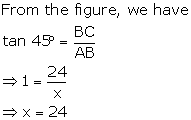
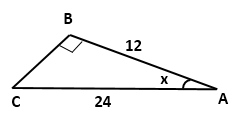
Question 3

Find the value of 'x' in each of the following:

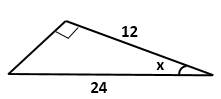
Solution 3

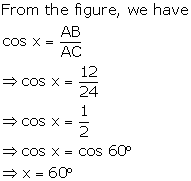
Question 4

Find the value of 'x' in each of the following:

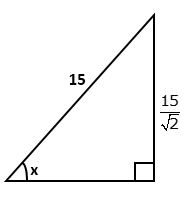
Solution 4

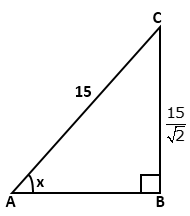
Question 5

Find the length of AD.

Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.

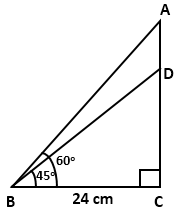
Solution 5

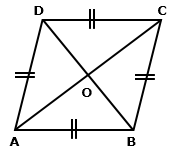
Question 6

Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.

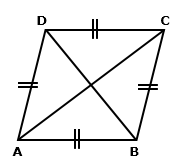
Solution 6

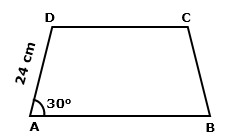
Question 7

In a trapezium ABCD, as shown, AB‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find:

length of AB

 

Solution 7

Construction: Draw DP ⊥ AB and CM ⊥ AB

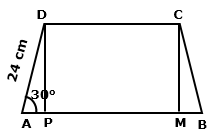
Question 8

Find the length of EC.

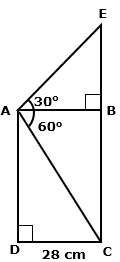
Solution 8

Question 9

In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:

a. AB

b. AC

c. AE

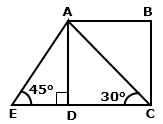
Solution 9

Question 10

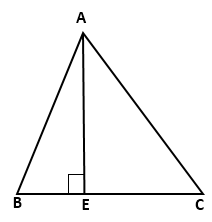
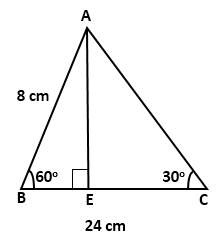
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:

a. BE

b. AC

Solution 10

Question 11

Find:

a. BC

b. AD

c. AC

Solution 11

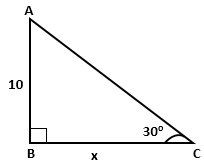
Question 12

Find the value 'x', if:

Solution 12

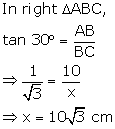
Question 13

Find the value 'x', if:

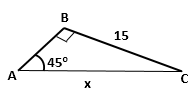
Solution 13

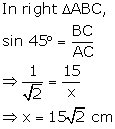
Question 14

Find the value 'x', if: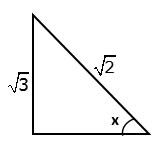

Solution 14

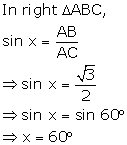
Question 15

Find the value 'x', if:

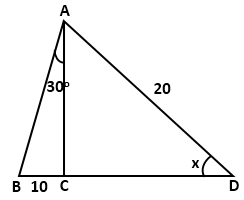
Solution 15

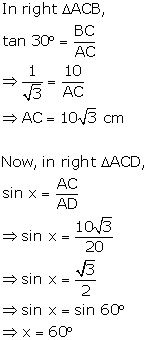
Question 16

Find the value 'x', if:

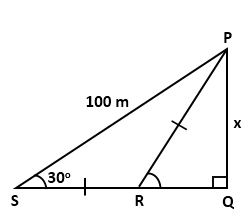
Solution 16

 

 

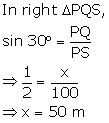
Question 17

Find the value 'x', if:

Solution 17

Question 18

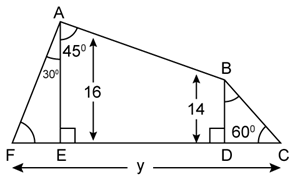
Solution 18

Construction: Draw BX ⊥ AE

Then, BD = EX = 14 cm and BX = ED

AX = AE - EX = 16 - 14 = 2

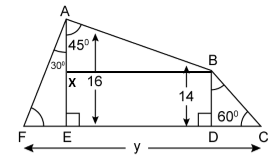
Question 19

 

Solution 19

Question 20

 

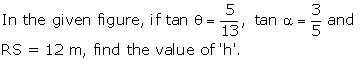
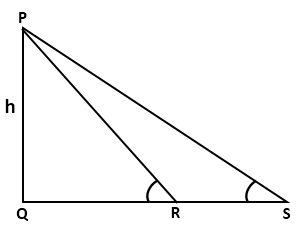
Solution 20

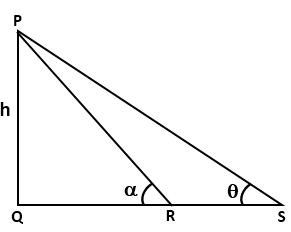
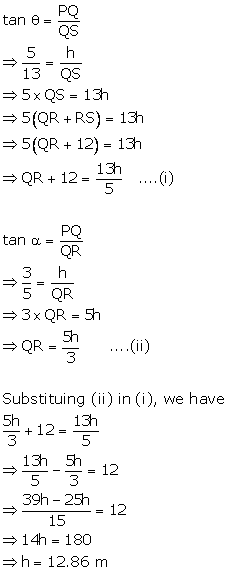
Question 21

Find x and y, in each of the following figure:

Solution 21

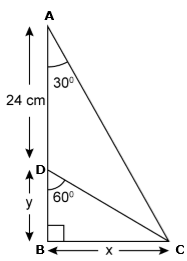
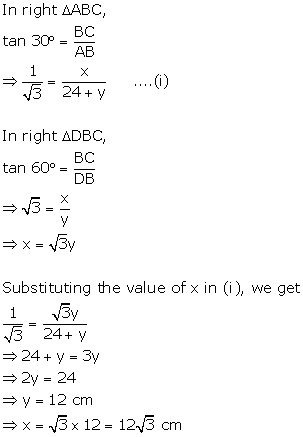
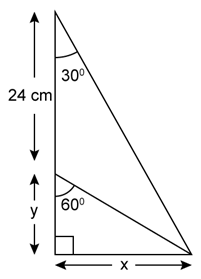
Question 22

Find x and y, in each of the following figure:

Solution 22

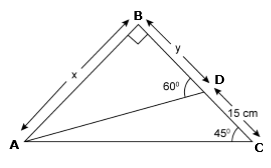
Question 23

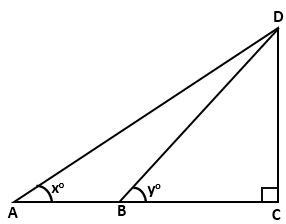
Solution 23

Question 24

Solution 24

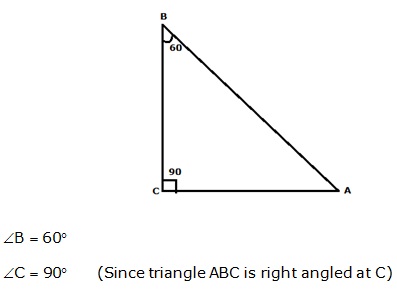
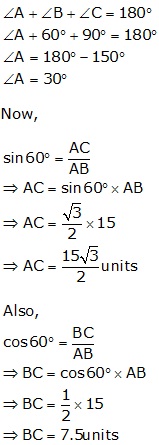
Question 25

Solution 25

2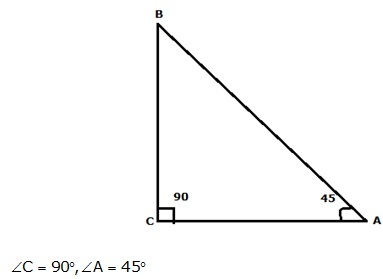

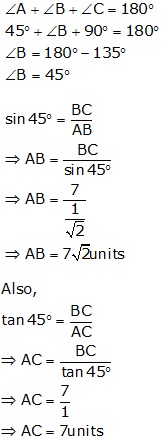
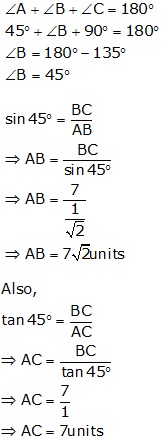
Question 26

Solution 26

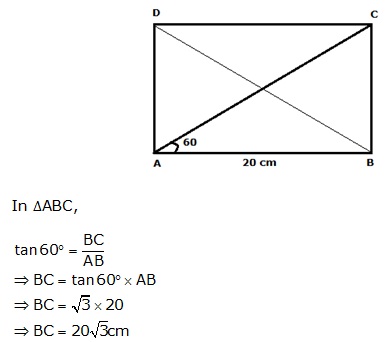
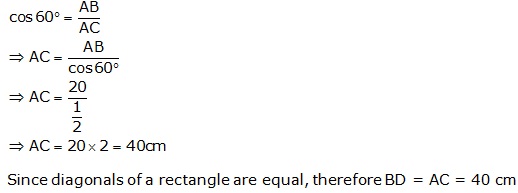
Question 27

In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:

Solution 27

Consider the following figure,

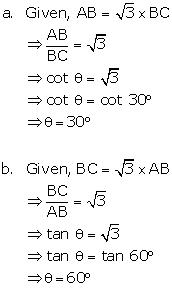
Question 28

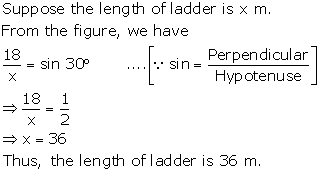
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.

Solution 28

Question 29

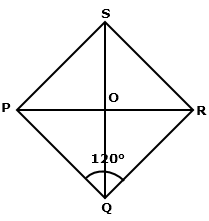
The perimeter of a rhombus is 100 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.

Solution 29

Consider the following figure,

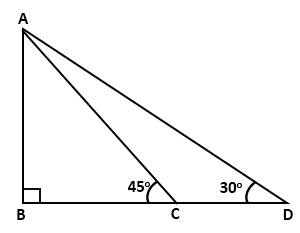
Question 30

In the given figure; ∠B = 90°, ∠ADB = 30°, ∠ACB = 45° and AB = 24 m.

Find the length of CD.

Solution 30

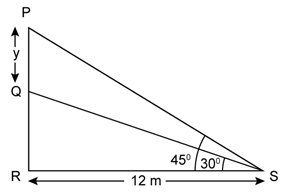
Question 31

In the given figure, a rocket is fired vertically upwards from its launching pad P. It first rises 20 km vertically upwards and then 20 km at 60° to the vertical. PQ represents the first stage of the journey and QR the second. S is a point vertically below R on the horizontal level as P, find:

a. the height of the rocket when it is at point R.

b. the horizontal distance of point S from P.

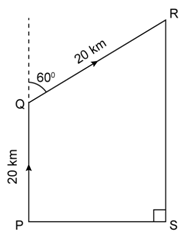
Solution 31

Draw QM ⊥ RS.

Clearly, ∠RQM = 30°  

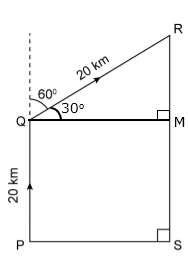
Chapter 27 - Trigonometrical Ratios of Standard Angles Exercise Ex. 27.3

Question 1

Evaluate the following:

Solution 1

Question 2

Evaluate the following:

Solution 2

Question 3

Evaluate the following:

Solution 3

Question 4

Evaluate the following:

Solution 4

Question 5

Evaluate the following:

Solution 5

Question 6

Evaluate the following:

Solution 6

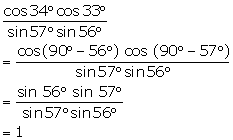
Question 7

Evaluate the following:

sin 31° - cos 59°

Solution 7

Question 8

Evaluate the following:

cot 27° - tan 63°

Solution 8

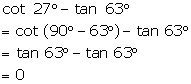
Question 9

Evaluate the following:

cosec 54° - sec 36°

Solution 9

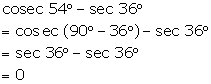
Question 10

Evaluate the following:

sin 28° sec 62° + tan 49° tan 41°

Solution 10

Question 11

Evaluate the following:

sec 16° tan 28° - cot 62° cosec 74°

Solution 11

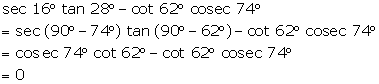
Question 12

Evaluate the following:

sin 22° cos 44° - sin 46° cos 68°

Solution 12

Question 13

Evaluate the following:

Solution 13

Question 14

Evaluate the following:

Solution 14

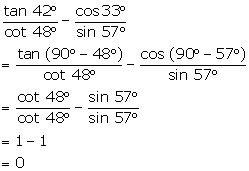
Question 15

Evaluate the following:

Solution 15

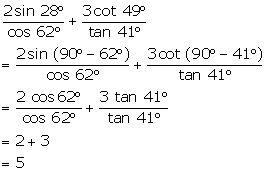
Question 16

Evaluate the following:

Solution 16

Question 17

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°:

sin 65° + cot 59°

Solution 17

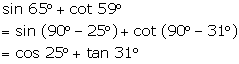
Question 18

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°:

cos 72° - cos 88°

Solution 18

Question 19

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°:

cosec 64° + sec 70°

Solution 19

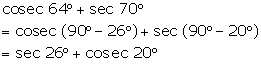
Question 20

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°:

tan 77° - cot 63° + sin 57°

Solution 20

Question 21

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°:

sin 53° + sec 66° - sin 50°

Solution 21

Question 22

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°:

cos 84° + cosec 69° - cot 68°

Solution 22

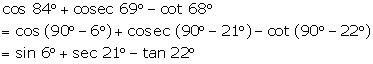
Question 23

Evaluate the following:

sin 35° sin 45° sec 55° sec 45°

Solution 23

Question 24

Evaluate the following:

cot 20° cot 40° cot 45° cot 50° cot 70°

Solution 24

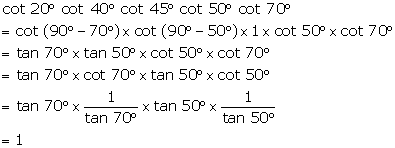
Question 25

Evaluate the following:

cos 39° cos 48° cos 60° cosec 42° cosec 51°

Solution 25

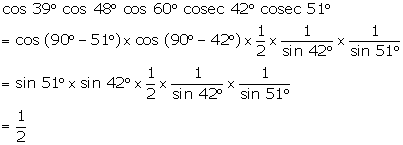
Question 26

Evaluate the following:

sin (35° + Ө) - cos (55° - Ө) - tan (42° + Ө) + cot (48° - Ө)

Solution 26

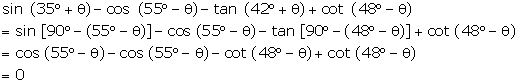
Question 27

Evaluate the following:

tan (78° + Ө) + cosec (42° + Ө) - cot (12° - Ө) - sec(48° - Ө)

Solution 27

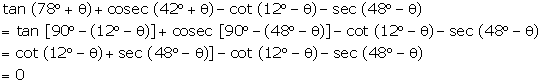
Question 28

Evaluate the following:

Solution 28

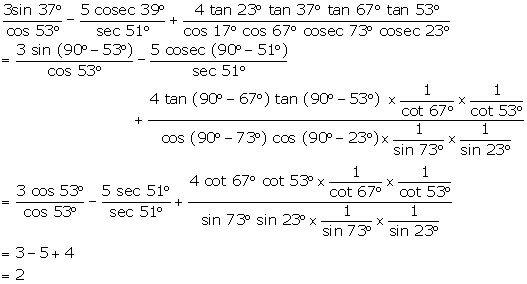
Question 29

Evaluate the following:

Solution 29

Question 30

Evaluate the following:

Solution 30

Question 31

Evaluate the following:

Solution 31

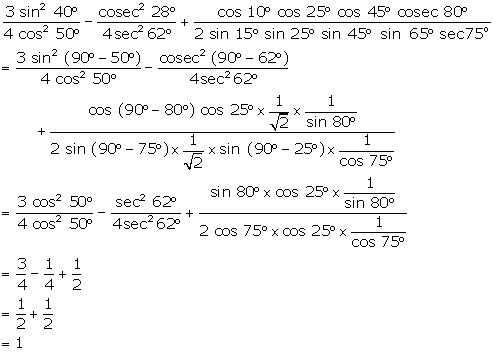
Question 32

Evaluate the following:

Solution 32

Question 33

If cos 3Ө = sin (Ө - 34°), find the value of Ө if 3Ө is an acute angle.

Solution 33

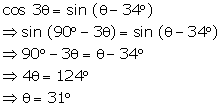
Question 34

If tan 4Ө = cot (Ө + 20°), find the value of Ө if 4Ө is an acute angle.

Solution 34

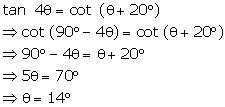
Question 35

If sec 2Ө = cosec 3Ө, find the value of Ө if it is known that both 2Ө and 3Ө are acute angles.

Solution 35

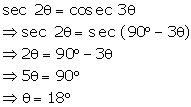
Question 36

If sin (Ө - 15°) = cos (Ө - 25°), find the value of Ө if (Ө -15°) and (Ө - 25°) are acute angles.

Solution 36

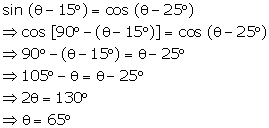
Question 37

Solution 37

Question 38

Solution 38

Question 39

If cosӨ = sin 60° and Ө is an acute angle find the value of 1- 2 sin²Ө

Solution 39

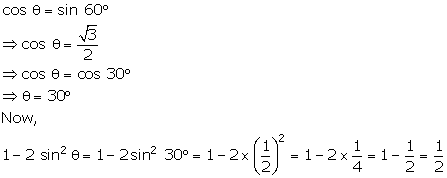
Question 40

If sec Ө = cosec 30° and Ө is an acute angle, find the value of 4 sin²Ө - 2 cos²Ө.

Solution 40

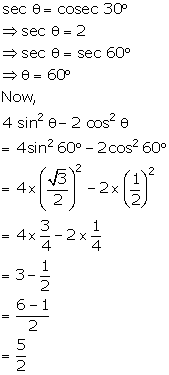
Question 41

Prove the following:

tan Ө tan (90° - Ө) = cot Ө cot (90° - Ө)

Solution 41

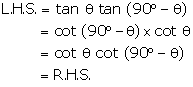
Question 42

Prove the following:

sin 58° sec 32° + cos 58° cosec 32° = 2

Solution 42

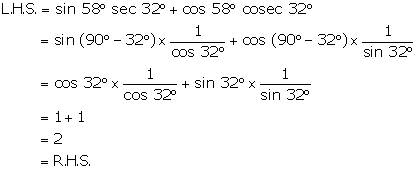
Question 43

Prove the following:

Solution 43

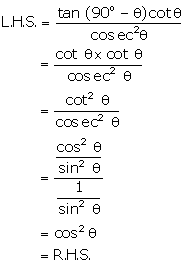
Question 44

Prove the following:

Solution 44

Question 45

If A + B = 90°, prove that

Solution 45