FRANK Solutions for Class 9 Maths Chapter 11 - Triangles and their congruency

Chapter 11 - Triangles and their congruency Exercise Ex. 11.1

Question 1

In the given figure, ∠Q : ∠R = 1 : 2. Find:

a. ∠Q

b. ∠R

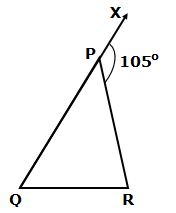
Solution 1

Question 2

The exterior angles, obtained on producing the side of a triangle both ways, are 100° and 120°. Find all the angles of the triangle.

Solution 2

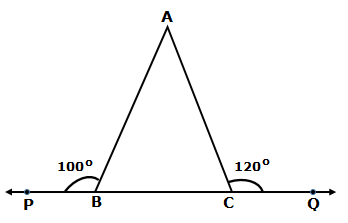
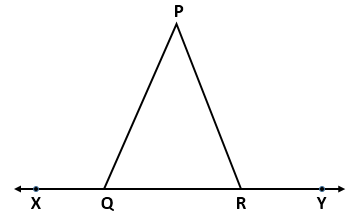
Question 3

Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.

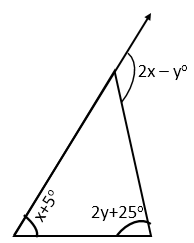
Solution 3

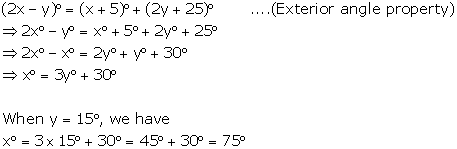
Question 4

In a triangle PQR, ∠P + ∠Q = 130° and ∠P + ∠R = 120°. Calculate each angle of the triangle.

Solution 4

Question 5

The angles of a triangle are (x + 10)°, (x + 30)° and (x - 10)°. Find the value of 'x'. Also, find the measure of each angle of the triangle.

Solution 5

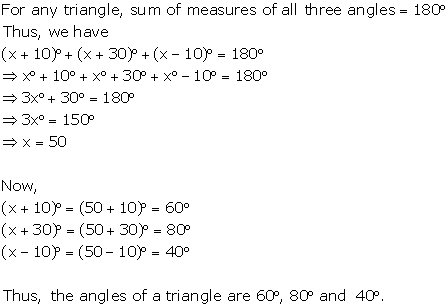
Question 6

Use the given figure to find the value of y in terms of p, q and r.

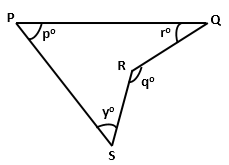
Solution 6

SR is produced to meet PQ at E.

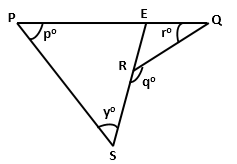
Question 7

In the figure given below, if RS is parallel to PQ, then find the value of ∠y.

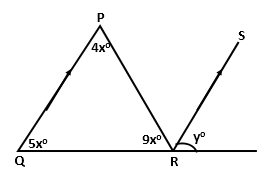
Solution 7

Question 8

In a triangle PQR, the internal bisectors of angles Q and R meet at A and the external bisectors of the angles Q and R meet at B. Prove that: ∠QAR + ∠QBR = 180°.

Solution 8

 

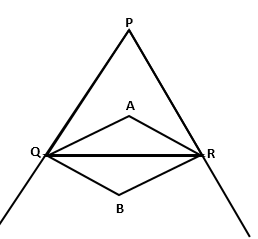
Question 9

Use the given figure to show that: ∠p + ∠q + ∠r = 360°.

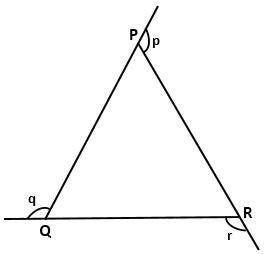
Solution 9

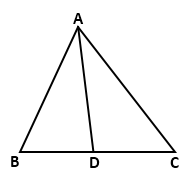
Question 10

In a triangle ABC. If D is a point on BC such that ∠CAD = ∠B, then prove that: ∠ADC = ∠BAC.

Solution 10

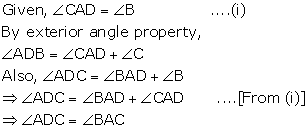
Question 11

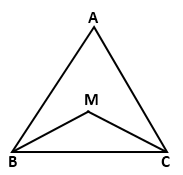
In a triangle ABC, if the bisectors of angles ABC and ACB meet at M then prove that: ∠BMC = 90° + 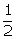∠A.

Solution 11

Question 12

If bisectors of angles A and D of a quadrilateral ABCD meet at 0, then show that ∠B + ∠C = 2 ∠AOD

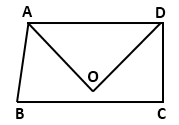
Solution 12

Question 13

If each angle of a triangle is less than the sum of the other two angles of it; prove that the triangle is acute-angled.

Solution 13

Question 14

If the angles of a triangle are in the ratio 2 : 4 : 6; show that the triangle is a right-angled triangle.

Solution 14

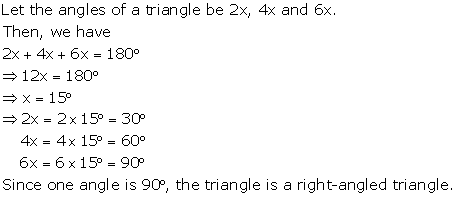
Question 15

In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.

Solution 15

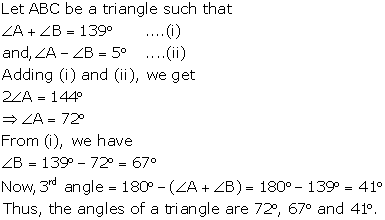
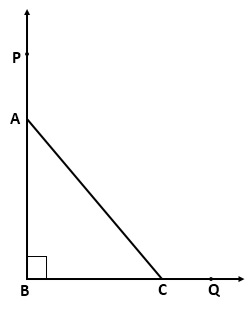
Question 16

In a right-angled triangle ABC, ∠B = 90°. If BA and BC produced to the points P and Q respectively, find the value of ∠PAC + ∠QCA.

Solution 16

Chapter 11 - Triangles and their congruency Exercise Ex. 11.2

Question 1

A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.

Solution 1

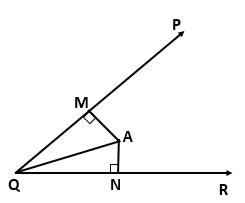
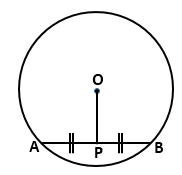
Question 2

In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.

Solution 2

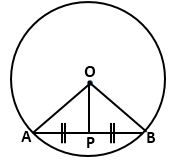
Question 3

In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.

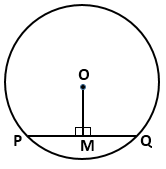
Solution 3

 

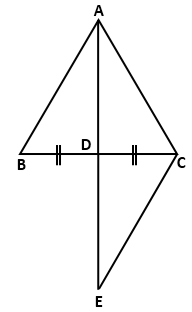
Question 4

In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:

a. DABD and DECD are congruent.

b. AB = EC

c. AB is parallel to EC

Solution 4

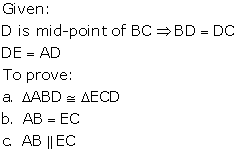
Question 5

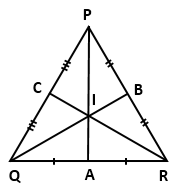
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P,Q,R to I are equal.

Solution 5

Question 6

In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:

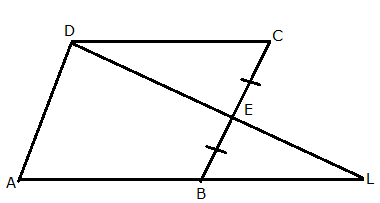
a. DDCE ≅ DLBE

b. AB = BL

c.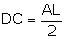  

Solution 6

Question 7

In the given figure, AB = DB and AC = DC. Find the values of x and y.

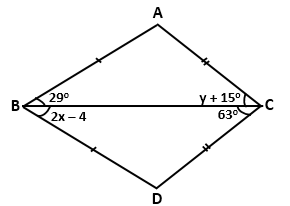
Solution 7

Question 8

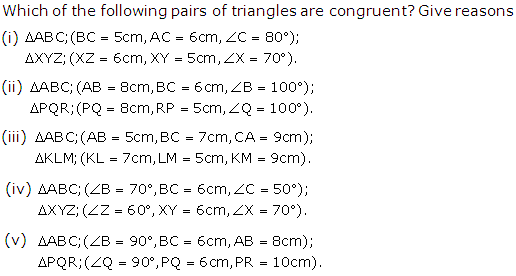
Solution 8

Question 9

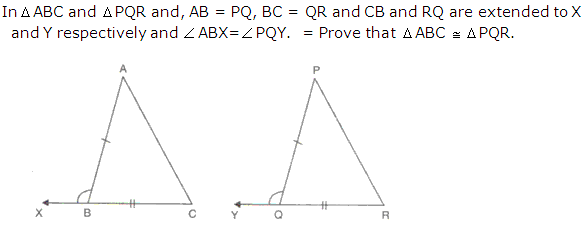
Solution 9

Question 10

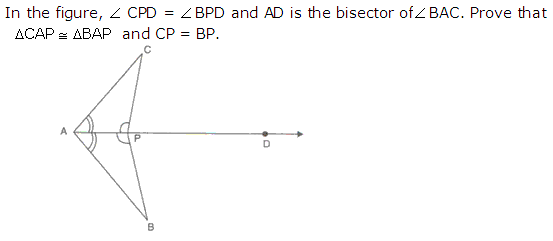
Solution 10

Question 11

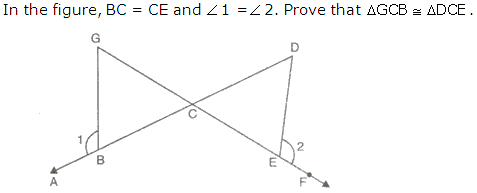
Solution 11

Question 12

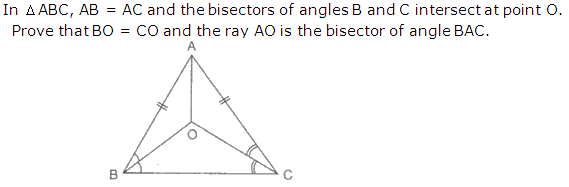
Solution 12

Question 13

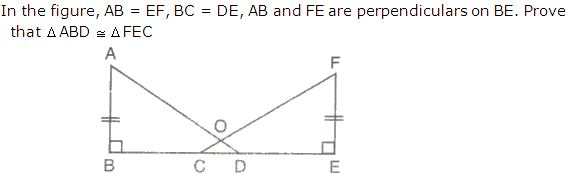
Solution 13

Question 14

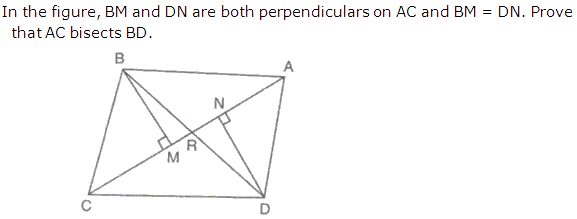
Solution 14

Question 15

Solution 15

Question 16

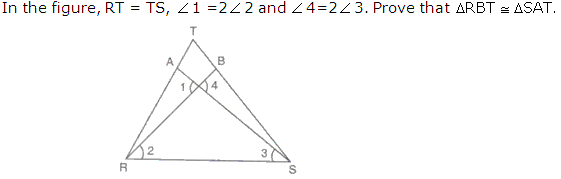
Solution 16

Question 17

Solution 17

Question 18

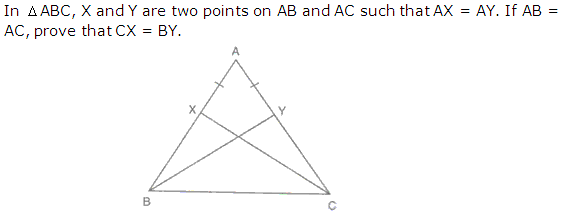
Solution 18

Question 19

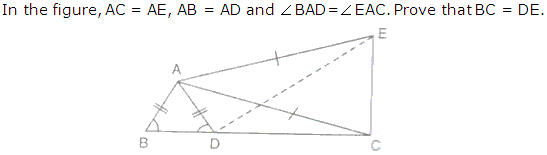
Solution 19

Question 20

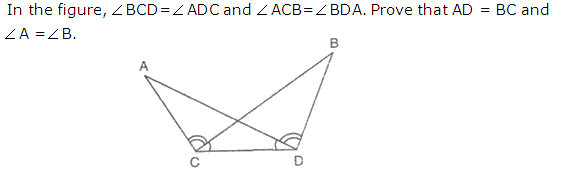
Solution 20

Question 21

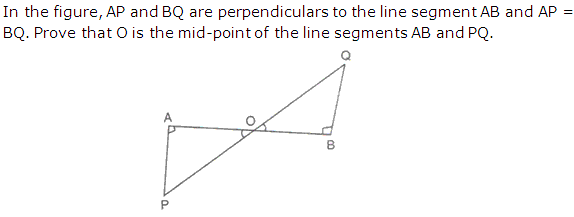
Solution 21

Question 22

Solution 22

Question 23

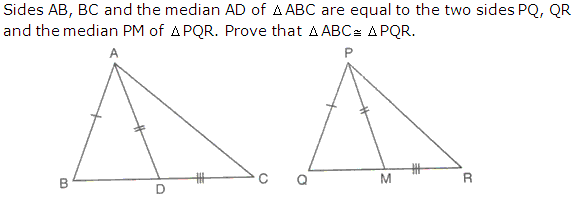
Solution 23

Question 24

Solution 24

Question 25

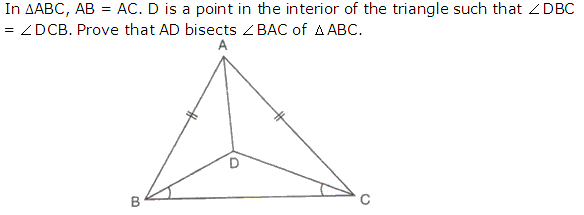
Solution 25

Question 26

Solution 26

Question 27

Solution 27

Question 28

Solution 28

Question 29

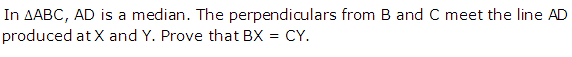
Solution 29

Question 30

Solution 30

Question 31

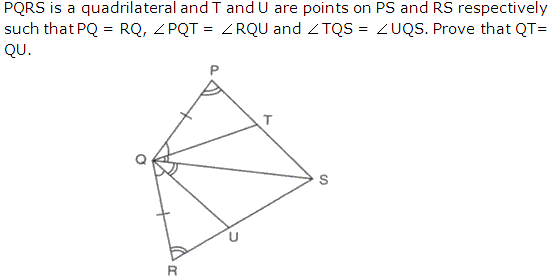
Solution 31