FRANK Solutions for Class 9 Maths Chapter 10 - Logarithms

FRANK Solutions for Class 9 Maths Chapter 10 - Logarithms

Chapter 10 - Logarithms Exercise Ex. 10.1

Question 1

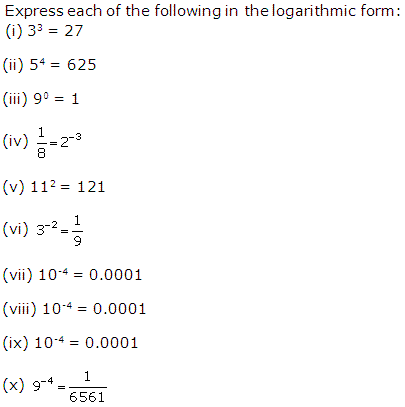
Solution 1

Question 2

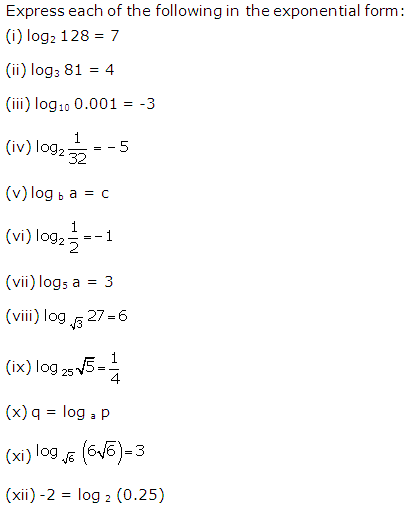
Solution 2

Question 3

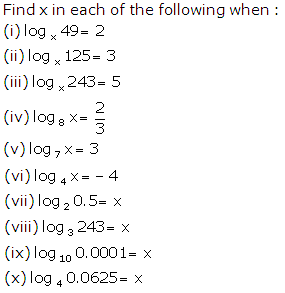
Solution 3

Question 4

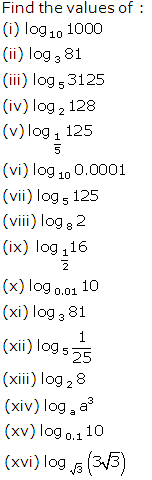
Solution 4

Question 5

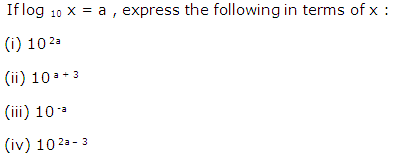
Solution 5

Question 6

Solution 6

Question 7

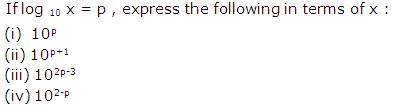
Solution 7

Question 8

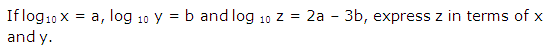
Solution 8

Question 9

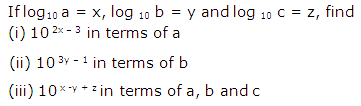
Solution 9

Question 10

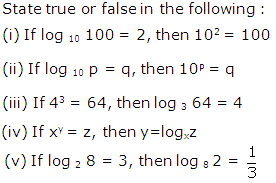
Solution 10

Chapter 10 - Logarithms Exercise Ex. 10.2

Question 1

Express log₁₀3 + 1 in terms of log₁₀x.

Solution 1

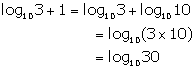
Question 2

State, true of false:

log (x + y) = log xy

Solution 2

False, since log xy = logx + logy

Question 3

State, true of false:

log 4 x log 1 = 0

Solution 3

True, since log 1= 0 and anything multiplied by 0 is 0.

Question 4

State, true of false:

log_ba =-log_ab

Solution 4

Question 5

 State, true of false:

 

Solution 5

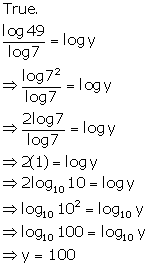
Question 6

If log 16 = a, log 9 = b and log 5 = c, evaluate the following in terms of a, b, c:

log 12

Solution 6

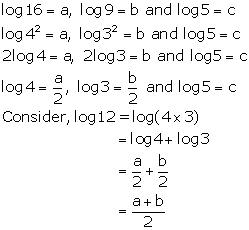
Question 7

If log 16 = a, log 9 = b and log 5 = c, evaluate the following in terms of a, b, c:

log 75

Solution 7

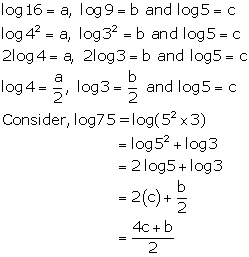
Question 8

If log 16 = a, log 9 = b and log 5 = c, evaluate the following in terms of a, b, c:

log 720

Solution 8

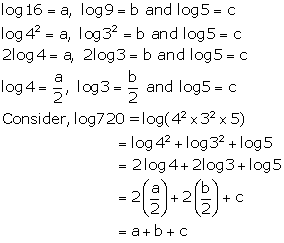
Question 9

If log 16 = a, log 9 = b and log 5 = c, evaluate the following in terms of a, b, c:

log 2.25

Solution 9

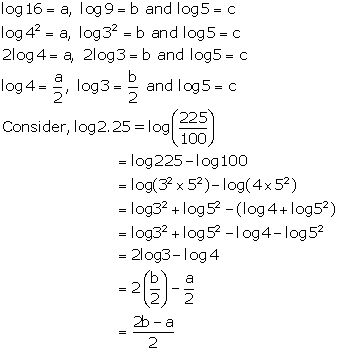
Question 10

If log 16 = a, log 9 = b and log 5 = c, evaluate the following in terms of a, b, c:

 

Solution 10

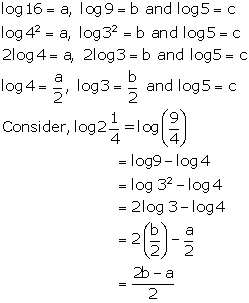
Question 11

 

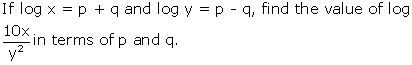
Solution 11

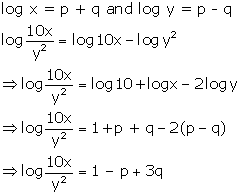
Question 12

If 2 log x + 1 = 40, find: x

Solution 12

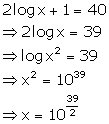
Question 13

If 2 log x + 1 = 40, find: log 5x

Solution 13

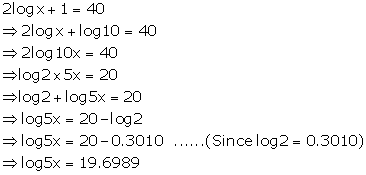
Question 14

If log₁₀25 = x and log₁₀27 = y; evaluate without using logarithmic tables, in terms of x and y:

log₁₀5

Solution 14

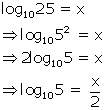
Question 15

If log₁₀25 = x and log₁₀27 = y; evaluate without using logarithmic tables, in terms of x and y:

log₁₀3

Solution 15

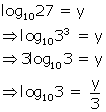
Question 16

Simplify:

log a² + log a^-1

Solution 16

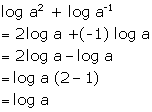
Question 17

Simplify:

log b ÷ log b²

Solution 17

Question 18

Find the value of:

 

Solution 18

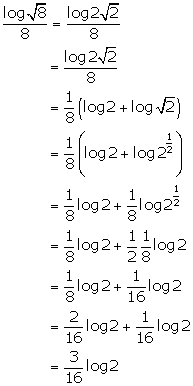
Question 19

Find the value of:

 

Solution 19

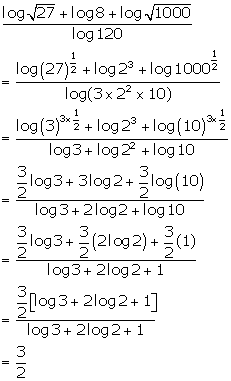
Question 20

Find the value of:

 

Solution 20

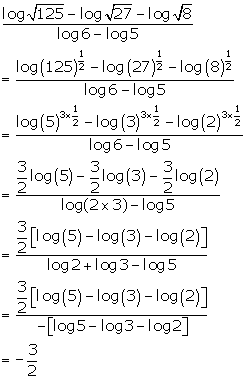
Question 21

 

Solution 21

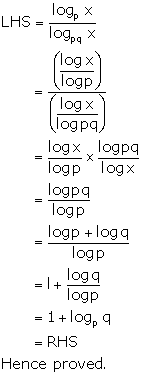
Question 22

Prove that:

Solution 22

Question 23

Prove that:

Solution 23

Question 24

 

Solution 24

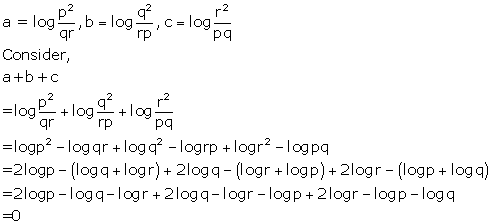
Question 25

If a = log 20 b = log 25 and 2 log (p - 4) = 2a - b, find the value of 'p'.

Solution 25

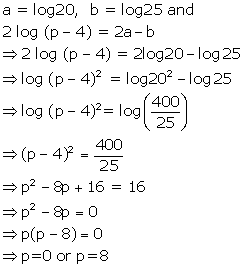
Question 26

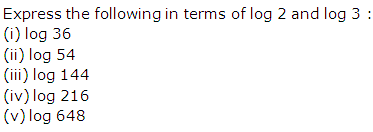
  (vi) log 12⁸

Solution 26

(vi)

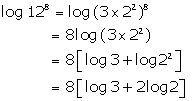
Question 27

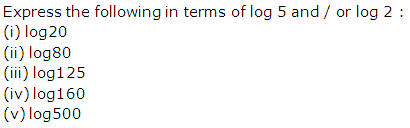
(vi) log 250

Solution 27

(vi)

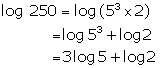
Question 28

   (vi)
          

Solution 28

(vi)
       

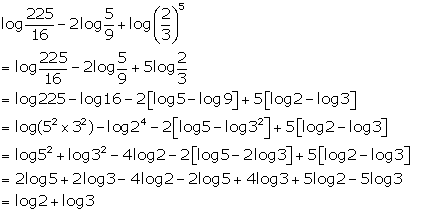
Question 29

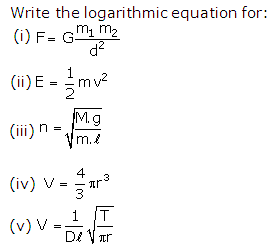
Solution 29

Question 30

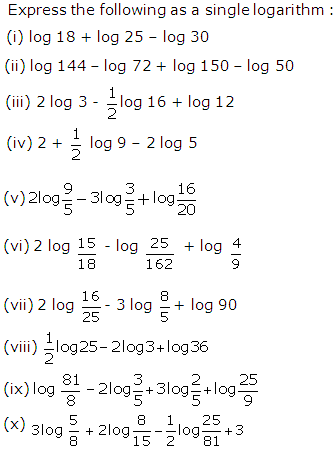
Solution 30

Question 31

Solution 31

Question 32

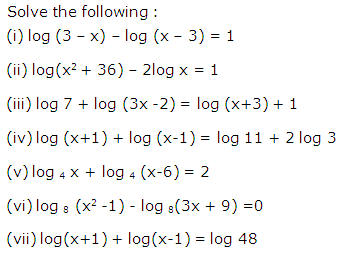
  (viii)

Solution 32

 (viii)
      

Question 33

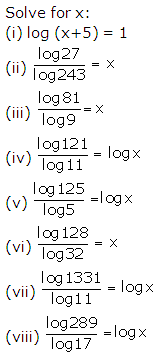
Solution 33

Question 34

Solution 34

Question 35

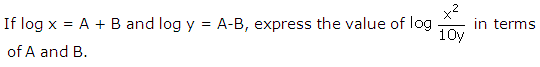
Solution 35

Question 36

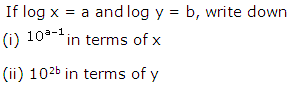
Solution 36

Question 37

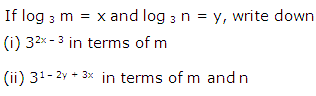
Solution 37

Question 38

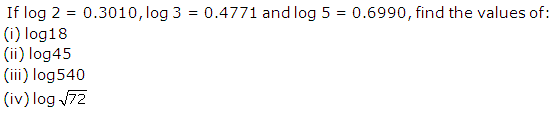
Solution 38

Question 39

Solution 39

Question 40

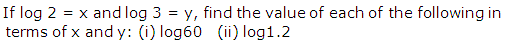
Solution 40

Question 41

Solution 41

Question 42

Solution 42

Question 43

Solution 43

Question 44

Solution 44

Question 45

Solution 45

Question 46

Solution 46

Question 47

Solution 47

Question 48

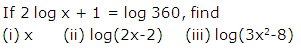
Solution 48

Question 49

Solution 49

Question 50

Solution 50

Question 51

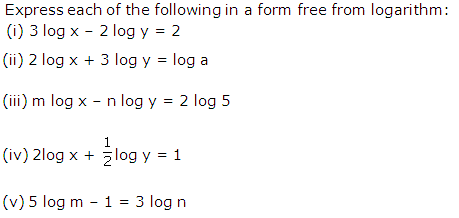
Solution 51

Question 52

Solution 52

Question 53

Solution 53

Question 54

Solution 54

Question 55

Solution 55

Question 56

Solution 56