Chapter 5 - Factorisation Exercise Ex. 5.1
Question 1
Factorise the
following by taking out the common factors:
4x2y3 - 6x3y2 -
12xy2
Solution 1
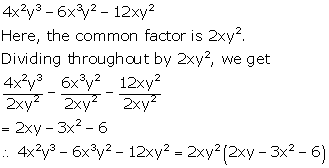
Question 2
Factorise the
following by taking out the common factors:
5a(x2 - y2) + 35b(x2 - y2)
Solution 2
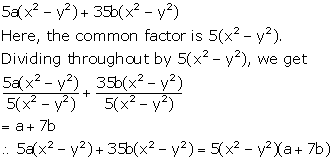
Question 3
Factorise the
following by taking out the common factors:
2x5y + 8x3y2 - 12x2y3
Solution 3
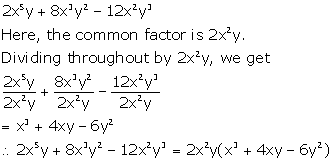
Question 4
Factorise the
following by taking out the common factors:
12a3 + 15a2b - 21ab2
Solution 4
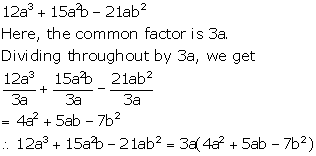
Question 5
Factorise the
following by taking out the common factors:
24m4n6 + 56m6n4
- 72m2n2
Solution 5

Question 6
Factorise the
following by taking out the common factors:
(a - b)2 -2(a - b)
Solution 6
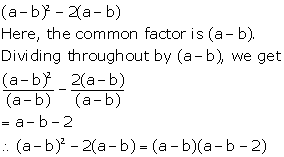
Question 7
Factorise the
following by taking out the common factors:
2a(p2 + q2) + 4b(p2 + q2)
Solution 7
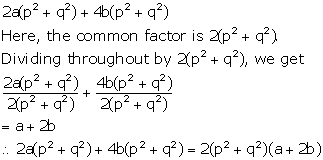
Question 8
Factorise the
following by taking out the common factors:
81(p + q)2 -9p - 9q
Solution 8
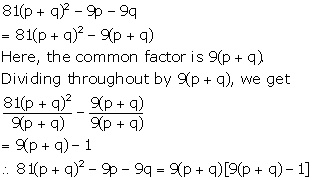
Question 9
Factorise the
following by taking out the common factors:
(mx + ny)2
+ (nx - my)2
Solution 9
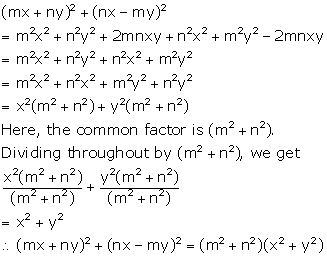
Question 10
Factorise the
following by taking out the common factors:
36(x + y)3 - 54(x + y)2
Solution 10
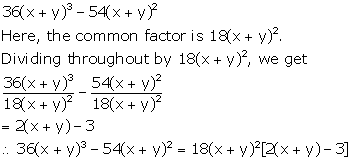
Question 11
Factorise the
following by taking out the common factors:
p(p2 + q2 - r2) + q(r2
- q2 -p2) - r(p2 + q2 - r2)
Solution 11
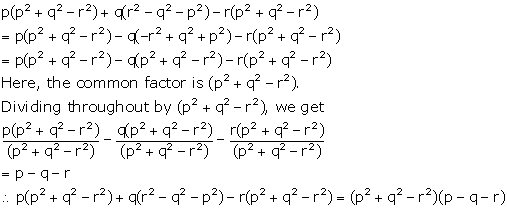
Question 12
Factorise the
following by grouping the terms:
15xy - 9x - 25y + 15
Solution 12
15xy - 9x - 25y + 15
= (15xy - 9x) - (25y + 15)
= 3x(5y - 3) - 5(5y - 3)
= (5y - 3)(3x - 5)
Question 13
Factorise the
following by grouping the terms:
15x2 + 7y - 3x - 35xy
Solution 13
15x2 + 7y - 3x - 35xy
= 15x2 - 3x - 35xy + 7y
= (15x2 - 3x) - (35xy - 7y)
= 3x(5x - 1) - 7y(5x - 1)
= (5x - 1)(3x - 7y)
Question 14
Factorise the
following by grouping the terms:
9 + 3xy + x2y + 3x
Solution 14
9 + 3xy + x2y + 3x
= 9 + 3xy + 3x + x2y
= (9 + 3xy) + (3x + x2y)
= 3(3 + xy) + y(3 + xy)
= (3 + xy)(3 + x)
Question 15
Factorise the
following by grouping the terms:
8(2a + b)2 - 8a -4b
Solution 15
8(2a + b)2 - 8a - 4b
= 8(2a + b)2 - (8a + 4b)
= 8(2a + b)2 - 4(2a + b)
= 4(2a + b)[2(2a + b) - 1]
= 4(2a + b)[4a + 2b - 1]
Question 16
Factorise the
following by grouping the terms:
x(x - 4)- x + 4
Solution 16
x(x - 4) - x + 4
= x(x - 4) - 1(x - 4)
= (x - 4)(x - 1)
Question 17
Factorise the
following by grouping the terms:
2m3 - 5n2 - 5m2n + 2mn
Solution 17
2m3 - 5n2 - 5m2n + 2mn
= 2m3 + 2mn - 5m2n - 5n2
= (2m3 + 2mn) - (5m2n + 5n2)
= 2m(m2 + n) - 5n(m2 + n)
= (m2 + n)(2m - 5n)
Question 18
Factorise the
following by grouping the terms:
4abx2 + 49aby2 + 14xy(a2 +
b2)
Solution 18
4abx2 + 49aby2 + 14xy(a2 +
b2)
= 4abx2 + 49aby2 + 14a2xy
+ 14b2xy
= (4abx2 + 14a2xy) + (14b2xy
+ 49aby2)
= 2ax(2bx + 7ay) + 7by(2bx + 7ay)
= (2bx + 7ay)(2ax + 7by)
Question 19
Factorise the
following by grouping the terms:
9x3 + 6x2y2 - 4y3
- 6xy
Solution 19
9x3 + 6x2y2 - 4y3
- 6xy
= 9x3 + 6x2y2 - 6xy - 4y3
= (9x3 + 6x2y2) - (6xy +
4y3)
= 3x2(3x + 2y2) - 2y(3x + 2y2)
= (3x + 2y2)(3x2 - 2y)
Question 20
Factorise the
following by grouping the terms:
3ax2 - 5bx2 + 9az2 + 6ay2
- 10by2 - 15bz2
Solution 20
3ax2 - 5bx2 + 9az2 + 6ay2
- 10by2 - 15bz2
= 3ax2 + 6ay2 + 9az2 - 5bx2
- 10by2 - 15bz2
= (3ax2 + 6ay2 + 9az2) -
(5bx2 + 10by2 + 15bz2)
= 3a(x2 + 2y2 + 3z2) -
5b(x2 + 2y2 + 3z2)
= (x2 + 2y2 + 3z2)(3a -
5b)
Question 21
Factorise the
following by grouping the terms:
8x3 - 24x2y + 54xy2 -162y3
Solution 21
8x3 - 24x2y + 54xy2 - 162y3
= (8x3 - 24x2y) + (54xy2 -
162y3)
= 8x2(x - 3y) + 54y2(x - 3y)
= (x - 3y)(8x2 + 54y2)
Question 22
Factorise the
following by grouping the terms:
2a + b + 3c - d + (2a + b)3 + (2a + b)2(3c
- d)
Solution 22
2a + b + 3c - d + (2a + b)3 + (2a + b)2(3c
- d)
= (2a + b + 3c - d) + [(2a + b)3 + (2a + b)2(3c
- d)]
= 1(2a + b + 3c - d) + (2a + b)2(2a + b + 3c -
d)
= (2a + b + 3c - d)[1 + (2a + b)2]
Question 23
Factorise the
following by grouping the terms:
xy(a2
+ 1) + a(x2 + y2)
Solution 23
xy(a2
+ 1) + a(x2 + y2)
= a2xy + xy + ax2
+ ay2
= (a2xy + ax2) + (ay2 + xy)
= ax(ay + x) + y(ay + x)
= (ay + x)(ax + y)
Question 24
Factorise the
following by grouping the terms:
p2x2 + (px2 + 1)x + p
Solution 24
p2x2 + (px2 + 1)x + p
= p2x2 + px3 + x + p
= (p2x2 + px3) + (p + x)
= px2(p + x) + 1(p + x)
= (p + x)(px2 + 1)
Question 25
Factorise the
following by grouping the terms:
x2 - (p + q)x + pq
Solution 25
x2 - (p + q)x + pq
= x2 - px - qx + pq
= (x2 - px) - (qx + pq)
= x(x - p) - q(x - p)
= (x - p)(x - q)
Question 26
Factorise the
following by grouping the terms:
Solution 26
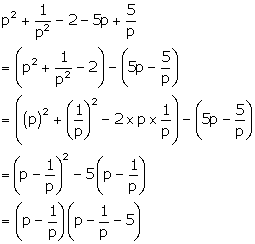
Question 27
Factorise the
following by grouping the terms:
x + y + m(x + y)
Solution 27
x + y + m(x + y)
= (x + y) + m(x + y)
= (x + y)(1 + m)
Question 28
Factorise the
following by grouping the terms:
Solution 28
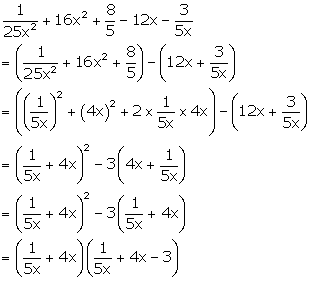
Question 29
Factorise the
following by grouping the terms:
2p(a2 - 2b2) -14p + (a2 -
2b2)2 - 7(a2 - 2b2)
Solution 29
2p(a2 - 2b2) - 14p + (a2 -
2b2)2 - 7(a2 - 2b2)
= 2p(a2 - 2b2) + (a2 - 2b2)2
- 14p - 7(a2 - 2b2)
= [2p(a2 - 2b2) + (a2 - 2b2)2]
- [14p + 7(a2 - 2b2)]
= (a2 - 2b2)(2p + a2 - 2b2)
- 7(2p + a2 - 2b2)
= (2p + a2 - 2b2)(a2 - 2b2
- 7)
Chapter 5 - Factorisation Exercise Ex. 5.2
Question 1
Factorise the
following by splitting the middle term:
x2 + 6x + 8
Solution 1
x2 + 6x + 8
= x2 + 4x + 2x + 8
= x(x + 4) + 2(x + 4)
= (x + 4)(x + 2)
Question 2
Factorise the
following by splitting the middle term:
x2 - 11x + 24
Solution 2
x2 - 11x + 24
= x2 - 8x - 3x + 24
= x(x - 8) - 3(x - 8)
= (x - 8)(x - 3)
Question 3
Factorise the
following by splitting the middle term:
x2 + 5x - 6
Solution 3
x2 + 5x - 6
= x2 + 6x - x - 6
= x(x + 6) - 1(x + 6)
= (x + 6)(x - 1)
Question 4
Factorise the
following by splitting the middle term:
p2- 12p - 64
Solution 4
p2 - 12p - 64
= p2 - 16p + 4p - 64
= p(p - 16) + 4(p - 16)
= (p - 16)(p + 4)
Question 5
Factorise the
following by splitting the middle term:
y2 - 2y - 24
Solution 5
y2 - 2y - 24
= y2 - 6y + 4y - 24
= y(y - 6) + 4(y - 6)
=(y - 6)(y + 4)
Question 6
Factorise the
following by splitting the middle term:
3x2 + 19x - 14
Solution 6
3x2 + 19x - 14
= 3x2 + 21x - 2x - 14
= 3x(x + 7) - 2(x + 7)
= (x + 7)(3x - 2)
Question 7
Factorise the
following by splitting the middle term:
15a2 - 14a - 16
Solution 7
15a2 - 14a - 16
= 15a2 - 24a + 10a - 16
= 3a(5a - 8) + 2(5a - 8)
= (5a - 8)(3a + 2)
Question 8
Factorise the
following by splitting the middle term:
12 + x - 6x2
Solution 8
12 + x - 6x2
= 12 + 9x - 8x - 6x2
= 3(4 + 3x) - 2x(4 + 3x)
= (4 + 3x)(3 - 2x)
Question 9
Factorise the
following by splitting the middle term:
7x2 + 40x - 12
Solution 9
7x2 + 40x - 12
= 7x2 + 42x - 2x - 12
= 7x(x + 6) - 2(x + 6)
= (x + 6)(7x - 2)
Question 10
Factorise the
following:
5x2 - 17xy + 6y2
Solution 10
5x2 - 17xy + 6y2
= 5x2 - 15xy - 2xy + 6y2
= 5x(x - 3y) - 2y(x - 3y)
= (x - 3y)(5x - 2y)
Question 11
Factorise the
following:
9x2 - 22xy + 8y2
Solution 11
9x2 - 22xy + 8y2
= 9x2 - 18xy - 4xy + 8y2
= 9x(x - 2y) - 4y(x - 2y)
= (x - 2y)(9x - 4y)
Question 12
Factorise the
following:
2x3 + 5x2y - 12xy2
Solution 12
2x3 + 5x2y - 12xy2
= 2x3 + 8x2y - 3x2y - 12xy2
= 2x2(x + 4y) - 3xy(x + 4y)
= (x + 4y)(2x2 - 3xy)
= (x + 4y)x(2x - 3y)
= x(x + 4y)(2x - 3y)
Question 13
Factorise the
following:
x2y2 + 15xy - 16
Solution 13
x2y2 + 15xy - 16
= x2y2 + 16xy - xy
- 16
= xy(xy
+ 16) - 1(xy + 16)
= (xy + 16)(xy
- 1)
Question 14
Factorise the
following:
(2p + q)2 - 10p - 5q - 6
Solution 14
(2p + q)2 - 10p - 5q - 6
= (2p + q)2 - (10p - 5q) - 6
= (2p + q)2 - 5(2p + q) - 6
= (2p + q)2 - 6(2p + q) + (2p + q) - 6
= (2p + q)(2p + q - 6) + 1(2p + q - 6)
= (2p + q - 6)(2p + q + 1)
Question 15
Factorise the
following:
y2 + 3y + 2 + by + 2b
Solution 15
y2 + 3y + 2 + by + 2b
= y2 + y + 2y + 2 + by + 2b
= y2 + y + by + 2y + 2 + 2b
= y(y + 1 + b) + 2(y + 1 + b)
= (y + 1 + b)(y + 2)
Question 16
Factorise the
following:
x3y3 - 8x2y2 +
15xy
Solution 16
x3y3 - 8x2y2 +
15xy
= x3y3 - 3x2y2
- 5x2y2 + 15xy
= x2y2(xy -
3) - 5xy(xy - 3)
= (xy - 3)(x2y2 - 5xy)
= (xy - 3)xy(xy - 5)
= xy(xy
- 3)(xy - 5)
Question 17
Factorise the
following:
Solution 17
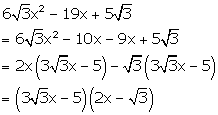
Question 18
Factorise the
following:
Solution 18
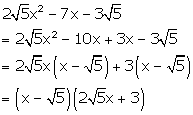
Question 19
Factorise the
following:
5(3x + y)2 + 6(3x + y) - 8
Solution 19
5(3x + y)2 + 6(3x + y) - 8
= 5(3x + y)2 + 10(3x + y) - 4(3x + y) - 8
= 5(3x + y)(3x + y + 2) - 4(3x + y + 2)
= (3x + y + 2)[5(3x + y) - 4]
Question 20
Factorise the
following:
5 - 4(a - b) - 12(a - b)2
Solution 20
5 - 4(a - b) - 12(a - b)2
= 5 - 10(a - b) + 6(a - b) - 12(a - b)2
= 5[1 - 2(a - b)] + 6(a - b)[1 - 2(a - b)]
= [5 + 6(a - b)][1 - 2(a - b)]
= (5 + 6a - 6b)(1 - 2a + 2b)
Question 21
Factorise the
following:
(3a - 2b)2 +3(3a - 2b) - 10
Solution 21
(3a - 2b)2 + 3(3a - 2b) - 10
= (3a - 2b)2 + 5(3a - 2b) - 2(3a - 2b) - 10
= (3a - 2b)(3a - 2b + 5) - 2(3a - 2b +5)
= (3a - 2b + 5)((3a - 2b - 2)
Question 22
Factorise the
following:
(a2 - 2a)2 - 23(a2 - 2a) +
120
Solution 22
(a2 - 2a)2 - 23(a2 - 2a) +
120
= (a2 - 2a)2 - 15(a2 - 2a)
- 8(a2 - 2a) + 120
= (a2 - 2a)(a2 - 2a - 15) - 8(a2
- 2a - 15)
= (a2 - 2a - 15)(a2 - 2a - 8)
= (a2 - 5a + 3a - 15)(a2 - 4a + 2a -
8)
= [a(a - 5) + 3(a - 5)][a(a - 4) + 2(a - 4)]
= [(a - 5)(a + 3)][(a - 4)(a + 2)]
= (a - 5)(a + 3)(a - 4)(a + 2)
= (a + 2)(a + 3)(a - 4)(a - 5)
Question 23
Factorise the
following:
(x + 4)2 - 5xy - 20y - 6y2
Solution 23
(x + 4)2 - 5xy - 20y - 6y2
= (x + 4)2 - 5y(x + 4) - 6y2
= (x + 4)2 - 6y(x + 4) + y(x + 4) - 6y2
= (x + 4)(x + 4 - 6y) + y(x + 4 - 6y)
= (x + 4 - 6y)(x + 4 + y)
= (x - 6y + 4)(x + y + 4)
Question 24
Factorise the
following:
7(x - 2)2 - 13(x - 2) - 2
Solution 24
7(x - 2)2 - 13(x - 2) - 2
= 7(x - 2)2 - 14(x - 2) + (x - 2) - 2
= 7(x - 2)(x - 2 - 2) + 1(x - 2 - 2)
= 7(x - 2)(x - 4) + 1(x - 4)
= (x - 4)[7(x - 2) + 1]
= (x - 4)(7x - 14 + 1)
= (x - 4)(7x - 13)
Question 25
Factorise the
following:
12 - (y + y2)(8 - y - y2)
Solution 25
12 - (y + y2)(8 - y - y2)
= 12 - a(8 - a) [Taking y + y2 = a]
= 12 - 8a + a2
= 12 - 6a - 2a + a2
= 6(2 - a) - a(2 - a)
= (2 - a)(6 - a)
= [2 - (y + y2)][6 - (y + y2)]
= (2 - y - y2)(6 - y - y2)
= (2 - 2y + y - y2)(6 - 3y + 2y - y2)
= [2(1 - y) + y(1 - y)][3(2 - y) + y(2 - y)]
= [(1 - y)(2 + y)][(2 - y)(3 + y)]
= (1 - y)(2 + y)(2 - y)(3 + y)
= (y - 1)(y + 2)(y - 2)(y + 3)
Question 26
Factorise the
following:
(p2 + p)2 - 8(p2 + p) + 12
Solution 26
(p2 + p)2 - 8(p2 + p) + 12
= (p2 + p)2 - 6(p2 + p) -
2(p2 + p) + 12
= (p2 + p)(p2 + p - 6) - 2(p2
+ p - 6)
= (p2 + p - 6)(p2 + p - 2)
= (p2 + 3p - 2p - 6)(p2 + 2p - p - 2)
= [p(p + 3) - 2(p + 3)][p(p + 2) - 1(p + 2)]
= [(p + 3)(p - 2)][(p + 2)(p - 1)]
= (p + 3)(p - 2)(p + 2)(p - 1)
Question 27
Factorise the
following:
(y2 - 3y)(y2 - 3y + 7) + 10
Solution 27
(y2 - 3y)(y2 - 3y + 7) + 10
= a(a + 7) + 10 [taking (y2 - 3y) = a]
= a2 + 7a + 10
= a2 + 5a + 2a + 10
= a(a + 5) + 2(a + 5)
= (a + 5)(a + 2)
= (y2 - 3y + 5)(y2 - 3y + 2)
= (y2 - 3y + 5)(y2 - 2y - y + 2)
= (y2 - 3y + 5)[y(y - 2) - 1(y - 2)]
= (y2 - 3y + 5)[(y - 2)(y - 1)]
= (y - 1)(y - 2)(y2 - 3y + 5)
Question 28
Factorise the
following:
(t2 - t)(4t2 - 4t - 5) - 6
Solution 28
(t2 - t)(4t2 - 4t - 5) - 6
= (t2 - t)[4(t2 - t) - 5] - 6
= a[4a - 5] - 6 [Taking (t2 - t) = a]
= 4a2 - 5a - 6
= 4a2 - 8a + 3a - 6
= 4a(a - 2) + 3(a - 2)
= (a - 2)(4a + 3)
= (t2 - t - 2)[4(t2 - t) + 3]
= (t2 - 2t + t - 2)(4t2 - 4t + 3)
= [t(t - 2) + 1(t - 2)](4t2 - 4t + 3)
= [(t - 2)(t + 1)](4t2 - 4t + 3)
= (t + 1)(t - 2)(4t2 - 4t + 3)
Question 29
Factorise the
following:
12(2x - 3y)2 - 2x + 3y - 1
Solution 29
12(2x - 3y)2 - 1(2x - 3y) - 1
= 12a2 - a - 1 [Taking (2x - 3y) = a]
= 12a2 - 4a + 3a - 1
= 4a(3a - 1) + 1(3a - 1)
= (3a - 1)(4a + 1)
= [3(2x - 3y) - 1][4(2x - 3y) + 1]
= (6x - 9y - 1)(8x - 12y + 1)
Question 30
Factorise the
following:
6 - 5x + 5y + (x - y)2
Solution 30
6 - 5x + 5y + (x - y)2
= 6 - 5(x - y) + (x - y)2
= 6 - 3(x - y) - 2(x - y) + (x - y)2
= 3[2 - (x - y)] - (x - y)[2 - (x - y)]
= 3(2 - x + y) - (x - y)(2 - x + y)
= (2 - x + y)(3 - x + y)
Question 31
Factorise the
following:
Solution 31
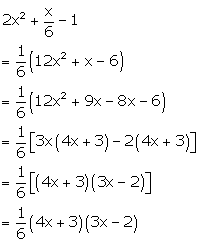
Question 32
Factorise the
following:
p4 + 23p2q2 + 90q4
Solution 32
P4 + 23p2q2 + 90q4
= p4 + 18p2q2 + 5p2q2
+ 90q4
= p2(p2 + 18q2) + 5q2(p2
+ 18q2)
= (p2 + 18q2)(p2 + 5q2)
Question 33
Factorise the
following:
2a3 + 5a2b - 12ab2
Solution 33
2a3 + 5a2b - 12ab2
= 2a3 + 8a2b - 3a2b - 12ab2
= 2a2(a + 4b) - 3ab(a + 4b)
= (a + 4b)(2a2 - 3ab)
= (a + 4b)a(2a - 3b)
= a(a + 4b)(2a - 3b)
Chapter 5 - Factorisation Exercise Ex. 5.3
Question 1
Factorise the
following by the difference of two squares:
x2 - 16
Solution 1
x2 - 16
= x2 - 42
= (x - 4)(x + 4)
Question 2
Factorise the
following by the difference of two squares:
64x2 - 121y2
Solution 2
64x2 - 121y2
= (8x)2 - (11y)2
= (8x - 11y)(8x + 11y)
Question 3
Factorise the
following by the difference of two squares:
441 - 81y2
Solution 3
441 - 81y2
= (21)2 - (9y)2
= (21 - 9y)(21 + 9y)
= 3(7 - 3y)3(7 + 3y)
= 9(7 - 3y)(7 + 3y)
Question 4
Factorise the
following by the difference of two squares:
x6 - 196
Solution 4
x6 - 196
= (x3)2 - (14)2
= (x3 - 14)(x3 + 14)
Question 5
Factorise the
following by the difference of two squares:
625 - b2
Solution 5
625 - b2
= (25)2 - (b)2
= (25 - b)(25 + b)
Question 6
Factorise the
following by the difference of two squares:
Solution 6
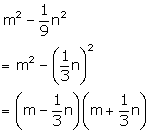
Question 7
Factorise the
following by the difference of two squares:
8xy2 - 18x3
Solution 7
8xy2 - 18x3
= 2x(4y2 - 9x2)
= 2x[(2y)2 - (3x)2]
= 2x[(2y - 3x)(2y + 3x)]
= 2x(2y - 3x)(2y + 3x)
Question 8
Factorise the
following by the difference of two squares:
16a4 - 81b4
Solution 8
16a4 - 81b4
= (4a2)2 - (9b2)2
= (4a2 - 9b2)(4a2 + 9b2)
= [(2a)2 - (3b)2](4a2 + 9b2)
= [(2a - 3b)(2a + 3b)](4a2 + 9b2)
= (2a - 3b)(2a + 3b)(4a2 + 9b2)
Question 9
Factorise the
following by the difference of two squares:
a(a - 1) - b(b - 1)
Solution 9
a(a - 1) - b(b - 1)
= a2 - a - b2 + b
= a2 - b2 - a + b
= (a2 - b2) - (a - b)
= (a - b)(a + b) - (a - b)
= (a - b)(a + b - 1)
Question 10
Factorise the
following by the difference of two squares:
(x + y)2 -1
Solution 10
(x + y)2 - 1
= (x + y)2 - (1)2
= (x + y + 1)(x + y - 1)
Question 11
Factorise the
following by the difference of two squares:
x2 + y2 - z2 - 2xy
Solution 11
x2 + y2 - z2 - 2xy
= x2 + y2 - 2xy - z2
= (x2 + y2 - 2xy) - z2
= (x - y)2 - (z)2
= (x - y - z)(x - y + z)
Question 12
Factorise the
following by the difference of two squares:
(x - 2y)2 -z2
Solution 12
(x - 2y)2 - z2
= (x - 2y)2 - (z)2
= (x - 2y - z)(x - 2y + z)
Question 13
Factorise the
following:
9(a - b)2 - (a + b)2
Solution 13
9(a - b)2 - (a + b)2
= [3(a - b)]2 - (a + b)2
= [3(a - b) - (a + b)][3(a - b) + (a + b)]
= (3a - 3b - a - b)(3a - 3b + a + b)
= (2a - 4b)(4a - 2b)
= 2(a - 2b)2(2a - b)
= 4(a - 2b)(2a - b)
Question 14
Factorise the
following:
25(x - y)2 - 49(c - d)2
Solution 14
25(x - y)2 - 49(c - d)2
= [5(x - y)]2 - [7(c - d)]2
= [5(x - y) - 7(c - d)][5(x - y) + 7(c - d)]
= (5x - 5y - 7c + 7d)(5x - 5y + 7c - 7d)
Question 15
Factorise the
following:
(2a - b)2 -9(3c - d)2
Solution 15
(2a - b)2 - 9(3c - d)2
= (2a - b)2 - [3(3c - d)]2
= [(2a - b) - 3(3c - d)][(2a - b) + 3(3c - d)]
= (2a - b - 9c + 3d)(2a - b + 9c - 3d)
Question 16
Factorise the
following:
b2 - 2bc + c2 - a2
Solution 16
b2 - 2bc + c2 - a2
= (b2 - 2bc + c2) - a2
= (b - c)2 - (a)2
= (b - c - a)(b - c + a)
Question 17
Factorise the
following:
Solution 17
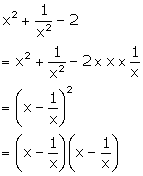
Question 18
Factorise the
following:
(x2
+ y2 - z2)2 - 4x2y2
Solution 18
(x2 + y2 - z2)2
- 4x2y2
= (x2 + y2 - z2)2
- (2xy)2
= (x2 + y2 - z2 - 2xy)(x2
+ y2 - z2 + 2xy)
= [(x2 + y2 - 2xy) - z2][(x2
+ y2 + 2xy) - z2]
= [(x - y)2 - z2][(x + y)2
- z2]
= [(x - y - z)(x - y + z)][(x + y - z)(x + y + z)]
= (x - y - z)(x - y + z)(x + y - z)(x + y + z)
Question 19
Factorise the
following:
a2 + b2 - c2 - d2
+ 2ab - 2cd
Solution 19
a2 + b2 - c2 - d2
+ 2ab - 2cd
= (a2 + b2 + 2ab) - (c2 +
d2 + 2cd)
= (a + b)2 - (c + d)2
= (a + b + c + d)(a + b - c - d)
Question 20
Factorise the
following:
4xy - x2 - 4y2 + z2
Solution 20
4xy - x2 - 4y2 + z2
= z2 - x2 - 4y2 + 4xy
= z2 - (x2 + 4y2 - 4xy)
= z2 - (x - 2y)2
= [z - (x - 2y)][z + (x - 2y)]
= (z - x + 2y)(z + x - 2y)
Question 21
Factorise the
following:
4x2 - 12ax - y2 - z2 - 2yz
+ 9a2
Solution 21
4x2 - 12ax - y2 - z2 - 2yz
+ 9a2
= (4x2 - 12ax + 9a2) - (y2
+ z2 + 2yz)
= (2x - 3a)2 - (y + z)2
= [(2x - 3a) + (y + z)][(2x - 3a) - (y + z)]
= (2x - 3a + y + z)(2x - 3a - y - z)
Question 22
Factorise the
following:
(x + y)3 - x - y
Solution 22
(x + y)3 - x - y
= (x + y)(x + y)2 - (x + y)
= (x + y)[(x + y)2 - 1]
= (x + y)[(x + y + 1)(x + y - 1)]
= (x + y)(x + y + 1)(x + y - 1)
Question 23
Factorise the
following:
y4 + y2 + 1
Solution 23
y4 + y2 + 1
= y4 + 2y2 + 1 - y2
= (y2 + 1)2 - y2
= (y2 + 1 + y)(y2 + 1 - y)
Question 24
Factorise the
following:
(a2 - b2)(c2 - d2)
- 4abcd
Solution 24
(a2 - b2)(c2 - d2)
- 4abcd
= a2c2 - a2d2 -
b2c2 + b2d2 - 4abcd
= a2c2 + b2d2 -
2abcd - a2d2 - b2c2 - 2abcd
= (a2c2 + b2d2
- 2abcd) - (a2d2 + b2c2 + 2abcd)
= (ac - bd)2 - (ad + bc)2
= [(ac - bd) + (ad + bc)][(ac - bd) - (ad + bc)]
= (ac - bd + ad + bc)(ac - bd - ad - bc)
Question 25
Express each of the following as the difference of two
squares:
(x2 - 2x + 3)(x2 + 2x + 3)
Solution 25
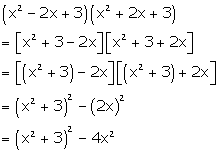
Question 26
Express each of the following as the difference of two squares:
(x2 - 2x + 3) (x2 - 2x - 3)
Solution 26
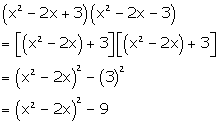
Question 27
Express each of the following as the difference of two
squares:
(x2 + 2x - 3) (x2 - 2x + 3)
Solution 27
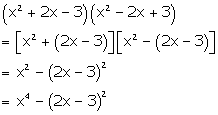
Question 28
Factorise:
Solution 28
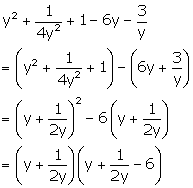
Question 29
Factorise:
Solution 29
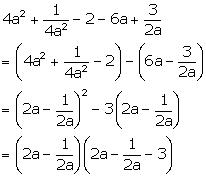
Question 30
Factorise:
x4 + y4 - 6x2y2
Solution 30
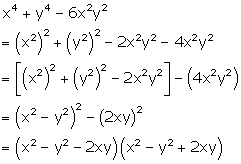
Question 31
Factorise:
4x4 + 25y4 + 19x2y2
Solution 31
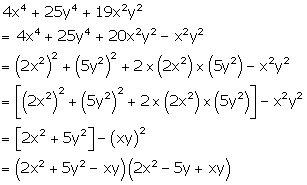
Question 32
Factorise:
Solution 32
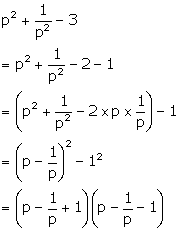
Question 33
Factorise:
5x2 - y2 - 4xy
+ 3x - 3y
Solution 33
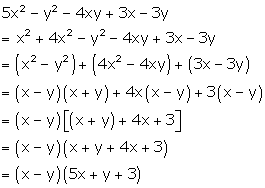

0 comments:
Post a Comment