FRANK Solutions for Class 9 Physics Chapter 2 - Motion in One Dimension

FRANK Solutions for Class 9 Physics Chapter 2 - Motion in One Dimension

Chapter 2 - Motion in One Dimension Exercise 61

Question 1

Define the state of rest.

Solution 1

A body is said to be in state of rest if it does not change its position with respect to its surrounding objects with time.

Question 2

Different positions of a body are given below. Which of the two positions lie on the same straight line?
(i) 8 m, 60^o NE
(ii) 3 m, 60^o NE
(iii) 5 m, 60^o EN
(iv) 5 m, 60^o NW

Solution 2

Out of these   positions, (i) and (ii) positions of body lie on same straight line as direction of these two are same.

Question 3

A quantity can be represented only when its magnitude and direction are specified. Is it scalar or vector?

Solution 3

A vector quantity is represented only when its magnitude and direction are specified so this quantity is a vector quantity.

Question 4

What do you mean by a vector quantity?

Solution 4

A vector quantity is that physical quantity which is represented by both magnitude and direction.

Question 5

Is mass a vector quantity?

Solution 5

No mass is not a vector quantity.

Question 6

How is a vector represented?

Solution 6

A vector is represented by an arrow. The length of the arrow represents  the magnitude of vector quantity and arrow head gives the direction of vector quantity.

Question 7

A book is lying in an almirah. Is it at rest or in motion?

Solution 7

If a book is lying in almirah then it is at rest.

Question 8

What do you mean by motion?

Solution 8

A body is said to be in motion when it change its position with respect to its surrounding objects with time.

Question 9

Are rest and motion relative?

Solution 9

Yes rest and motion are relative to each other.

Question 10

Out of force and energy, which one is vector?

Solution 10

Out of Force and Energy, Force is a vector quantity.

Question 11

Give two examples of scalars.

Solution 11

Examples of scalars are distance and mass.

Chapter 2 - Motion in One Dimension Exercise 62

Question 1

Are the passengers sitting in a train in motion or at rest with respect to each other?

Solution 1

Passengers sitting in a train are at rest with respect to each other.

Question 2

You are at rest as well as in motion. Justify the statement giving your point of view.

Solution 2

Yes we are at rest as well as motion because we are at rest with respect to a observer which is itself at rest and we are in motion with respect to a observer which is in motion.

Question 3

A train is moving out of a railway station. Is the platform at rest or in motion with respect to the moving train? Justify your answer.

Solution 3

The platform is in motion with respect to train. As train is moving with respect to platform so platform would also look in motion with respect to train.

Question 4

Represent the location of an object described as at 15 m, 45^o west of north, on a graph paper.

Solution 4

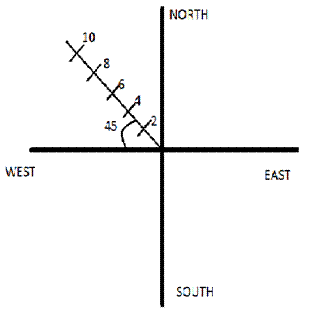
Question 5

Represent the position of a body described as at 15 m, 30^o north of west, on a graph paper.

Solution 5

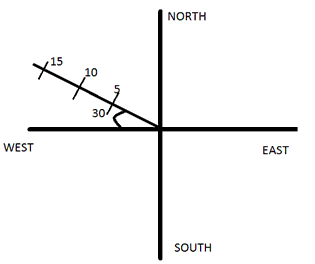
Question 6

Name the physical quantity representing the magnitude and its direction.

Solution 6

The physical quantity representing the magnitude and its direction is a vector quantity.

Question 7

Answer the following questions:
(i) Can we add two scalars?
(ii) Can we add two vectors?
(iii) Can we multiply two scalars?
(iv) Can we add a scalar quantity to a vector quantity?
(v) Can we subtract two scalars?
(vi) Can we subtract a scalar quantity from a vector quantity? Is the reverse true?
(vii) Can we multiply vectors?

Solution 7

(i) Yes we can add two scalars.
(ii) Yes we can add two vectors.
(iii) Yes we can multiply two scalars.
(iv) No we cannot add a scalar quantity to a vector quantity.
(v) Yes we can subtract two scalars.
(vi) No we cannot subtract a scalar quantity from a vector quantity. Reverse is also not true.
(vii) Yes we can multiply vectors.

Question 8

What do you mean by the distance traveled by a body?

Solution 8

The actual length of the path covered by a moving object irrespective of its direction of motion is called the distance travelled by the object.

Question 9

Can distance covered by a body be less than the magnitude of its displacement?

Solution 9

No the distance covered by a body cannot be less than the magnitude of its displacement.

Question 10

Define displacement.

Solution 10

The displacement of a moving body is defined as the change in its position along a particular direction

Question 11

Write the SI units for measurement of distance and displacement.

Solution 11

SI unit for measurement  of distance and diplacement is metre denoted by m.

Question 12

Show the difference between distance and displacement with the help of a diagram.

Solution 12

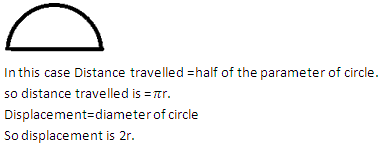
Question 13

Can a body have negative displacement?

Solution 13

Yes a body can have negative displacement.

Question 14

Under what condition is the displacement of a body equal to the distance traveled by it?

Solution 14

If a body is moving in a straight line then the displacement of a body is equal to the distance travelled by it.

Question 15

Write two differences between distance and displacement.

Solution 15

(i) Distance is a scalar quantity whereas displacement is a vector quantity.
(ii) Distance is always positive but displacement can be negative,zero or positive.

Question 16

Calculate the distance and displacement in the following cases:

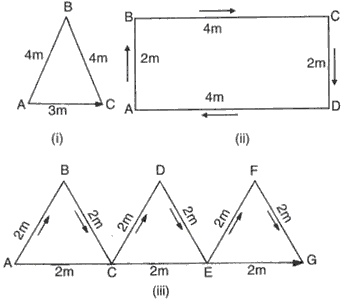
Solution 16

(i) Distance is 4+4=8 m while displacement is 3m.
(ii) Distance is 2+4+2+4=12m while displacement is 0m.
(iii) Distance is 2+2+2+2+2+2=12m while displacement is 2+2+2=6m.

Question 17

Solution 17

Question 18

Ashok starts from his house and travels 3 km to reach his school. On finding the school gates closed, he returns to his house. What is?
(i) The distance traveled by Ashok and
(ii) The displacement of Ashok?

Solution 18

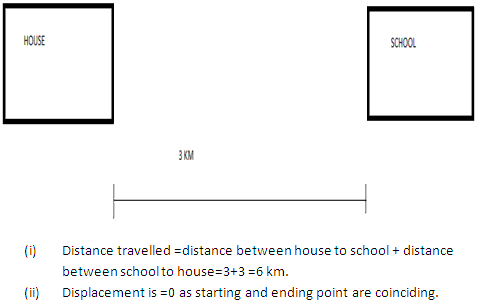
Question 19

A satellite makes a complete round along its circular orbit. What is its displacement?

Solution 19

Question 20

An object is thrown vertically upwards. It rises upto a height H and then returns to its initial position. Calculate (i) The total distance traveled by the object, (ii) The displacement of the object.

Solution 20

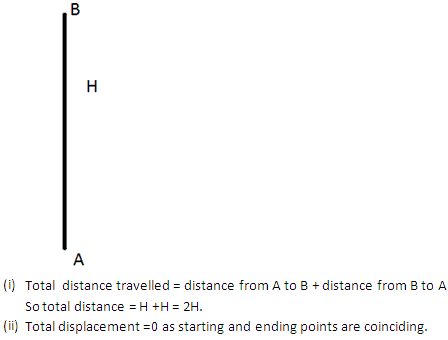
Chapter 2 - Motion in One Dimension Exercise 79

Question 1

Define speed of a body.

Solution 1

Speed of a body can be defined as distance covered by the body in unit time.

Question 2

Arrange the following speeds in the increasing order:
(i) A bicycle moving with a speed of 36 km/h.
(ii) A car moving with a speed of 2 km/min.
(iii) An athlete running with a speed of 7 m/s.

Solution 2

we convert all the speeds in m/s to compare them.
36 km/hr = (36 X 1000)/3600 = 10m/s.
2 km/min = (2 X 1000)/60 = 33.3 m/s.
7 m/s = 7 m/s.
So increasing order of speed is 7m/s < 10m/s <33m/s.

Question 3

A boy covers half of his journey with a uniform speed of u and the other half with a uniform speed of v. What is the average speed for the whole journey?

Solution 3

let  total distance be S.
Boy covers distance S/2  with speed  u then time taken by him to cover this distance would be T₁ =S/2u.
Again boy covers rest of the distance S/2 with speed v then time taken by him to cover this distance would be T₂  =S/2v.
So total time taken by boy to cover the distance S is T = T₁ + T₂.
Total time T= S/2 (1/u +1/v) = s(u+v)/2uv.
And average speed  = S/T = 2uv/(u+v).

Question 4

Does uniform speed mean constant speed?

Solution 4

Yes uniform speed and constant speed have same meaning.

Question 5

A body goes from P to Q with a uniform speed of u and immediately returns back to P at a uniform speed of v. What is the average speed for the whole journey?

Solution 5

let S be the distance between P and Q.
Body covers forward journey distance S  (P to Q) with speed  u then time taken by him to cover this distance would be T₁ =S/u.
Again body covers backward journey distance S (Q to P) with speed v then time taken by him to cover this distance would be T₂  =S/v.
So total time taken by body to cover the distance S is T = T₁ + T₂.
Total time T= S (1/u +1/v) = s(u+v)/uv.
And average speed  = 2S/T = 2uv/(u+v).

Question 6

In Q. 13 above, what is the average velocity for the whole journey?

Solution 6

As body goes from P to Q and then return back to P so the displacement of the body would be zero and hence average velocity would also be zero.

Question 7

A car travels from P to Q at a uniform speed of 20 ms^-1 and immediately turns back and travels towards Q with a uniform speed of 30 ms^-1. What is the average speed for the whole journey?

Solution 7

let distance between P and Q is S.
Speed of car while travelling from P to Q is 20 m/s.
Let car take time T₁ to travel from P to Q then T₁= S/20.
Speed of car while travelling from Q to P is 30 m/s.
Let car take time T₂ to travel from Q to P  then T₂= S/30.
Total time = T₁ + T₂ =  S/20 +S/30 =S/12.
So average speed of journey = total distance/ total time = 2S/(S/12) = 24 m/s.
Average speed of journey is 24 m/s.

Question 8

How does speed differ from velocity?

Solution 8

Speed is a scalar quantity whereas velocity is a vector quantity. So speed doesn't have its direction and velocity has a particular direction.

Question 9

When do the speed and velocity of a moving body become equal?

Solution 9

Speed and velocity of a moving body become equal when the body moves in a straight line.

Question 10

What is meant by a constant velocity? Is it same as uniform velocity?

Solution 10

When the velocity of a moving body doesn't change with time then the velocity of the body is said to be constant or uniform.Yes uniform velocity and constant velocity are one and the same thing.

Question 11

Define acceleration.

Solution 11

Acceleration of a body is rate of change of its velocity with respect to the time.

Question 12

What do you understand by the average speed of a body?

Solution 12

Average speed of a body can be defined as ratio of total distance covered by a body In total time.

Question 13

What is the SI unit of acceleration?

Solution 13

SI unit of acceleration is ms^-2.

Question 14

Write the SI units of speed and average speed.

Solution 14

Both speed and average speed  have same unit and that is ms^-1.

Question 15

Do speed and average speed of a body have the same meaning?

Solution 15

No speed and average speed  of a body have different meaning.

Question 16

Which is greater?
(i) 60 km/hr
(ii) 15 m/s

Solution 16

60 km/hr can be converted into m/s to compare with 15m/s.
60 km/hr = (60 X 1000)/3600 = 16.66 m/s. so speed 60 km/hr is greater.

Question 17

Convert 20 m/s into km/hr.

Solution 17

20m/s can be converted inti km/hr as
20 m/s = (20 X 3600)/1000 = 72 km/hr.

Question 18

Which is greater?
(i) 36 km/hr
(ii) 8.5 m/s

Solution 18

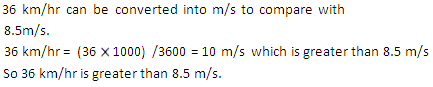
Question 19

What are the SI units of velocity?

Solution 19

SI unit of velocity is ms^-1.

Question 20

Two cars are moving with speeds of 40 km/hr due North and 40 km/hr due South respectively. Do they have the same velocity?

Solution 20

No as their direction is different  they don't have same velocity.

Chapter 2 - Motion in One Dimension Exercise 80

Question 1

The acceleration of a moving body is constant in magnitude and direction. Must the path of the body be a straight line? If not, given an example.

Solution 1

If the acceleration of a moving body is constant in magnitude and direction then the path of the body must not be a straight line because in circular motion also acceleration of a body is constant in magnitude and always directed towards the centre.
So the path of the body may be a straight line and may be a circular one.

Question 2

Solution 2

No the relation S = v X t cannot used to find the total distance covered by a body moving with non-uniform speed.

Question 3

The area under a speed-time graph in a given intervals gives the total distance covered by a body irrespective of its motion being uniform or non-uniform.

Solution 3

Yes area under a speed time graph in a given interval gives the total distance covered by a body.

Question 4

The area of the right triangle under a speed-time graph is 500 m, in a time interval of 20 s. What is the speed of the body? Is the motion uniform or non-uniform?

Solution 4

Yes the motion is uniform and the uniform speed is given by area under speed time graph divided by time interval.
So speed = 500/20 =25 m/s.

Question 5

What does a positive acceleration mean?

Solution 5

Positive acceleration corresponds to situation when velocity is continuously increasing with respect to the time.

Question 6

What does a negative acceleration mean?

Solution 6

Negative acceleration corresponds to situation when velocity is continuously decereasing with respect to the time.

Question 7

A body falls towards the earth. Does it have positive or negative acceleration?

Solution 7

If a body falls towards earth then it would have a positive  acceleration.

Question 8

The acceleration of a body is 8.5 ms^-2. What does this statement mean?

Solution 8

If a body has acceleration of 8.5 ms^-2 then it means its velocity is increasing at a rate of 8.5 ms^-1 per second.

Question 9

Write the SI unit of retardation.

Solution 9

SI unit of retardation is ms^-2.

Question 10

A car traveling at 60 km/h, stops on applying brakes in 10 seconds. What is its acceleration?

Solution 10

first convert 60 km/h in m/s.
60 km/hr =(60 X 1000)/3600 = 16.7 m/s.
This is initial velocity of car i.e u = 16.7 m/s.
As car stops in 10 seconds so final velocity is =0 m/s.
So acceleration = (v-u)/t = (0-16.7)/10 = -1.67 ms^-2.
Acceleration of car is = -1.67 ms^-2.

Question 11

A quantity is measured to be -30 m/s. Is it speed or velocity?

Solution 11

-30 m/s is speed.

Question 12

Give the name of the physical quantity that corresponds to the rate of change of displacement.

Solution 12

Velocity corresponds to the rate of change of displacement.

Question 13

Can the speed of a body be negative?

Solution 13

No the speed of a body cannot be negative.

Question 14

What kind of a velocity does a flying bird most likely to have?
(a) Uniform velocity, or
(b) Non- uniform velocity.

Solution 14

A flying bird most likely to have a non uniform velocity.

Question 15

Find the initial velocity of a car which is stopped in 10 seconds by applying brakes. Retardation due to brakes is 2.5 ms^-2.

Solution 15

Let initial velocity be u.
Final velocity is v= 0 m/s.
Time taken by body to come to rest = 10 sec.
Retardation =2.5 ms^-2.
We know v = u +at.
Then u = v - at.
u = 0 - (-2.5 X 10) = 25 m/s.
So initial velocity of the body is 25 m/s.

Question 16

What do you understand by the equations of motion?

Solution 16

Equation of motion gives us the picture of motion of moving body.

Question 17

Write down the three equations of motion.

Solution 17

First equation of motion is v = u + at.
Second equation of motion is s= ut + 1/2a t².
Third eqution of motion is v² - u² =2as.

Question 18

How many variables are present in each equation of motion?

Solution 18

Four variables are present in each equation of motion.

Question 19

What are the uses of equations of motion?

Solution 19

Four variables are present in each equation of motion and if any of three is known to us then fourth can be easily find with the help of these equation of motion.

Question 20

Write the SI unit of acceleration and retardation.

Solution 20

SI unit of acceleration and retardation is ms^-2.

Question 21

Name the physical quantity which is equal to the area under speed-time graph.

Solution 21

Distance is the physical quantity  which is equal to the area under speed-time graph.

Question 22

Distinguish between uniformly and non-uniformly accelerated motions.

Solution 22

A uniformly accelerated motion is one in which speed is constantly increasing or decreasing with time while a non uniform motion is one in which speed is not constantly changing with time.

Question 23

Can you use the relation[B₁]?

Solution 23

No we cannot use this relation for a body moving with uniform acceleration.

Question 24

How does the slope of a speed-time graph give the acceleration of a body moving along a straight line?

Solution 24

Slope of a graph is given as rate of change of y coordinates to the x coordinate. In speed time graph speed is on the y axis and time is on the x axis. And we define acceleration as rate of change of speed with respect to time. So slope of a speed time graph gives acceleration.

Question 25

Give two examples of uniform circular motion from your daily life.

Solution 25

(i) Motion of blades of an electric fan.
(ii) Motion of moon around earth.

Question 26

How will you use a speed-time graph to find whether the acceleration of the body is uniform or not?

Solution 26

A straight line curve on speed time graph indicates that acceleration of the body is uniform  and a zigzag or curved line indicates that acceleration of a body is not uniform.

Question 27

The graph of one quantity versus another result in a straight line. How are the quantities related to each other?

Solution 27

Two quantities are directly proportional to each other.

Question 28

A car travels at a uniform speed of 42 km/h. In 10 minutes, how much distance would it cover?

Solution 28

As we distance = speed  X  time.
Speed = 42 km/hr.
Time = 10 m = 1/6 hr.
Distance = 42 X 1/6 =7 km.

Question 29

The initial velocity of a car is 10 ms^-1. It moves with an acceleration of 2 ms^-2. What will be its speed after 10 seconds?

Solution 29

Initial velocity u =10 ms^-1.
Acceleration a = 2 ms^-2.
Time t = 10 s.
By using first equation of motion
V = u + at.
V = 10 + 2 X 10.
V (final velocity) = 30 ms^-1.

Question 30

The speed of a car increases from 10 km/h to 64 km/h in 10 seconds. What will be its acceleration?

Solution 30

Initial velocity u = 10 km/hr. = (10 X 1000)/3600 = 8.33 ms^-1.
Final velocity = 64 km/hr = (64 X 1000)/3600 = 17.77 ms^-1.
Time = 10 s.
Acceleration = (v-u)/t = (17.77- 8.33)/10 = 9.44/10 = 0.94 ms^-2.

Chapter 2 - Motion in One Dimension Exercise 81

Question 1

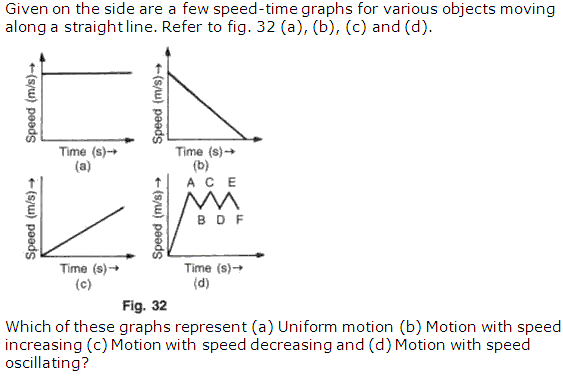
Solution 1

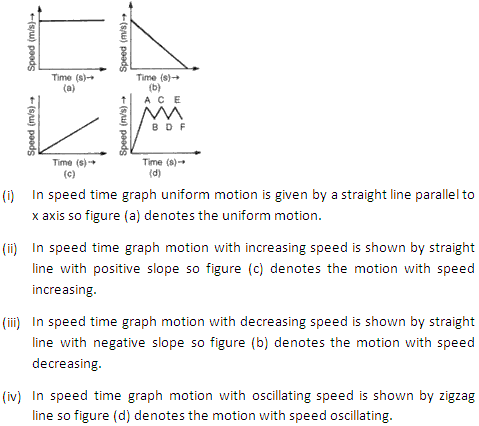
Question 2

Can a body have negative speed?

Solution 2

No a body cannot have a speed negative.

Question 3

Is distance covered during nth second more than the distance covered in n seconds?

Solution 3

No₂ distance covered by body during n_th second is not more than the distance covered in n seconds.

Question 4

Draw the speed-time graph of a body when its initial speed is not zero and the speed increases uniformly with time.

Solution 4

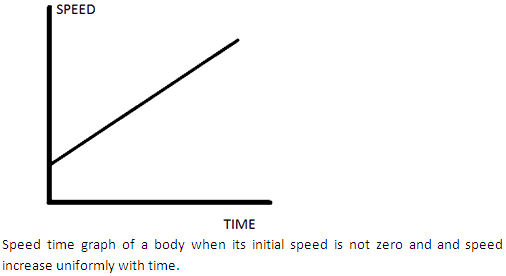
Question 5

Draw the speed-time graph of a body starting from some point P, gradually picking up speed, then running at a uniform speed and finally slowing down to stop at some point Q.

Solution 5

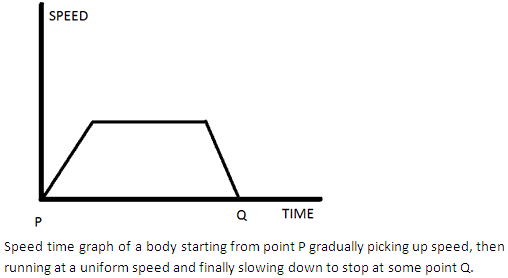
Question 6

What can you conclude if the speed-time graph of a body is a curve moving upwards starting from the origin?

Solution 6

If speed time graph is moving upward then the body is accelerating and if it is starting from origin then it means the body has initial velocity =0.

Question 7

What can you conclude if the speed-time graph of a body is a straight line sloping upwards and not passing through the origin?

Solution 7

Speed time graph is moving upward then the body is accelerating and if it is not starting from origin then it means the body has some initial velocity.

Question 8

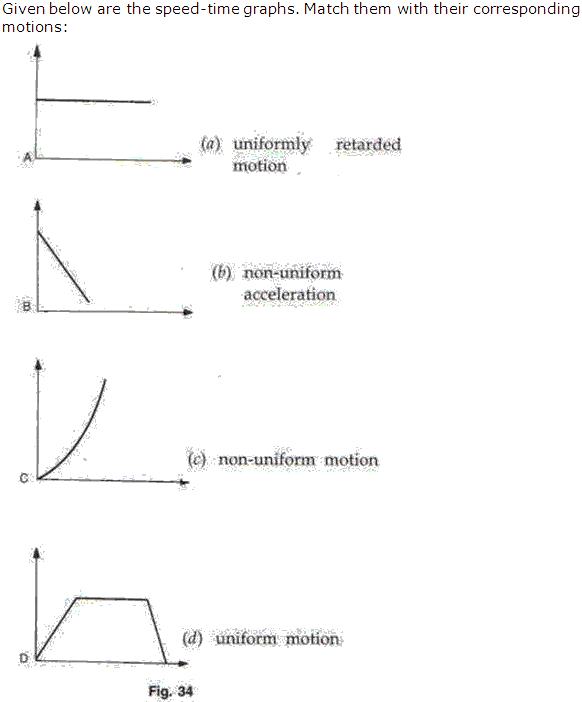
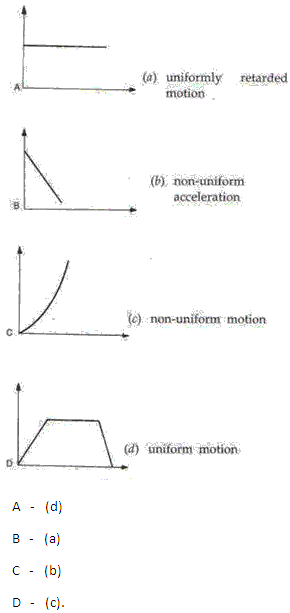
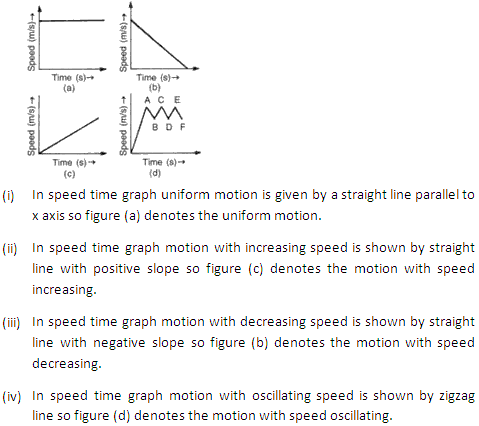
Draw the following graphs:
(i) Speed versus time for a stepped motion.
(ii) Speed versus time for a non-uniform acceleration.
(iii) Distance versus time for a body at rest.
(iv) Speed versus time for a fluctuating speed.
(v) Speed versus time for a uniformly retarded motion.

Solution 8

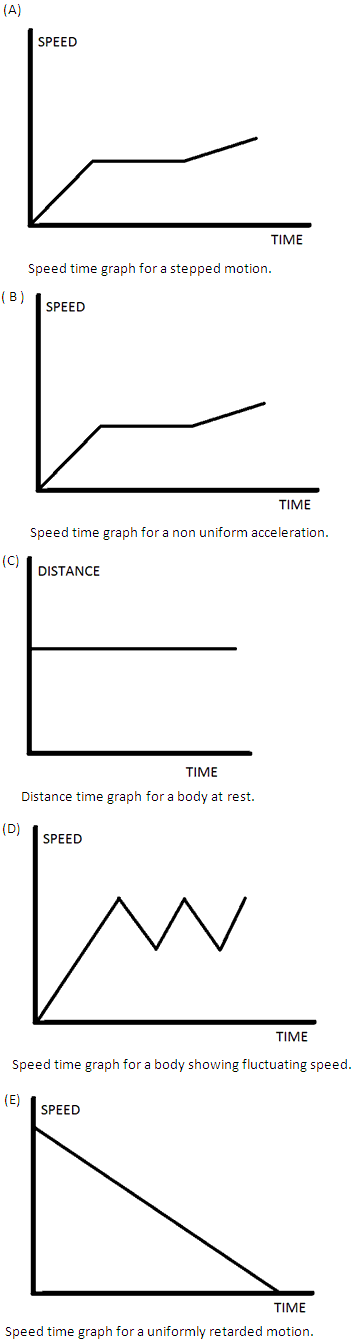
Question 9

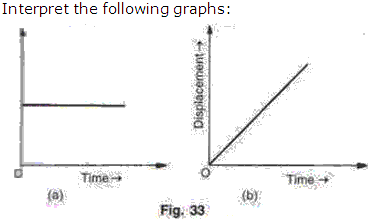
Solution 9

Question 10

Solution 10

Question 11

Derive the equations (i) v= u+at and (ii) v²-u²= 2as, where the symbols have their usual meanings.

Solution 11

Question 12

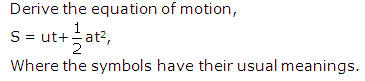
Solution 12

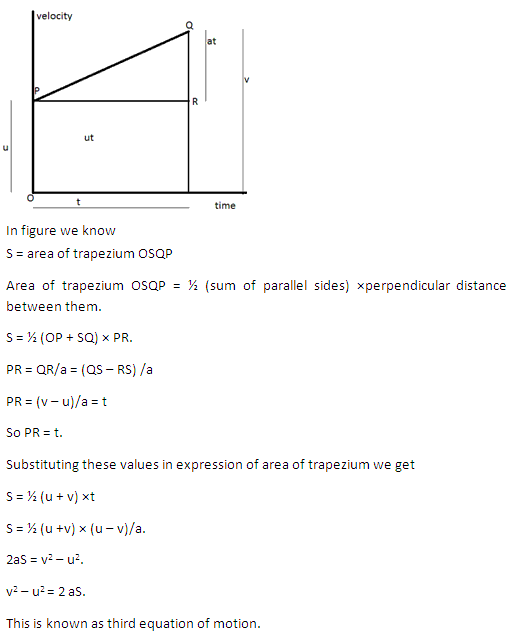
Chapter 2 - Motion in One Dimension Exercise 83

Question 1

Write two examples of vectors.

Solution 1

Displacement and velocity are two examples of vectors.

Question 2

The distance covered by a body is directly proportional to the square of the time elapsed. What can you say about its acceleration?

Solution 2

This means the body has a positive acceleration.

Question 3

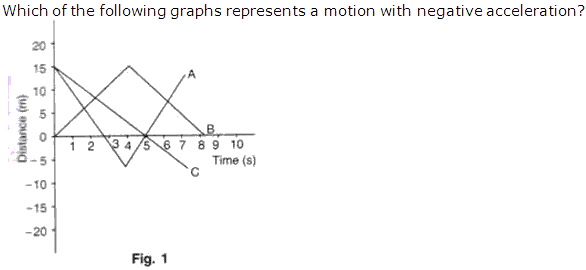
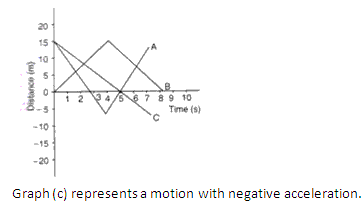
Solution 3

Question 4

State which of the following situations are possible:
(a) A body moving with constant acceleration but with Zero velocity.
(b) A body moving horizontally with an acceleration in vertical direction.
(c) A body moving with a constant velocity in an accelerated motion.

Solution 4

(i) No a body with constant acceleration cannot have a zero velocity.
(ii) No a body with an acceleration in vertical direction cannot move horizontally.
(iii) No in an accelerated motion a body cannot have a constant velocity.

Question 5

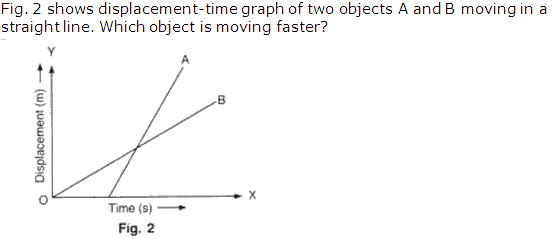
Solution 5

Question 6

What can you say about the nature of motion of a body of its displacement-time graph is
(a) A straight line parallel to line axis?
(b) A straight line inclined to the time axis with an acute angle?

Solution 6

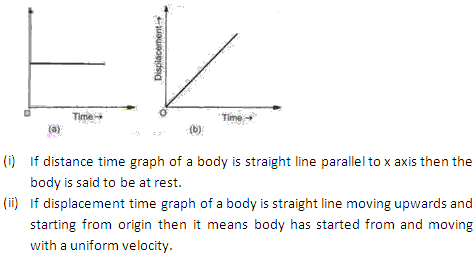
(i) In displacement-time graph a straight line parallel to time axis shows that body is at rest position.
(ii) In displacement-time graph a straight line inclined to the time axis with an acute angle means body is moving with a positive velocity.

Question 7

Is it possible for an accelerating body to have constant speed?

Solution 7

No a accelerating body cannot have constant speed.

Question 8

What can you say about the motion of a body if
(a) Its time-displacement graph is a straight line.
(b) Its time-velocity graph is a straight line?

Solution 8

(i) In displacement-time graph a straight line shows body is at rest if it is parallel to time axis and shows a body is moving with uniform velocity if it is inclined to x axis.
(ii) In velocity-time graph a straight line shows body is moving with uniform constant velocity if it is parallel to x axis and shows body is moving constant acceleration of it is inclined to x axis.

Question 9

Is the average speed during different time intervals for a uniform motion the same or different?

Solution 9

Average speed during different time intervals for a uniform motion is same.

Question 10

What is the velocity of a stone thrown vertically upwards at its maximum height?

Solution 10

Velocity of a stone thrown vertically upward at its maximum height is Zero.

Question 11

Why does the velocity of a stone thrown vertically upwards decreases?

Solution 11

Velocity of a stone  thrown vertically upwards decrease because acceleration due to gravity is acting on downward direction.

Question 12

Write the SI unit of retardation.

Solution 12

SI unit of retardation is ms^-2.

Question 13

What is the relation between linear velocity and linear speed?

Solution 13

Linear velocity would be equal to linear speed if body is moving in a straight line.

Question 14

Draw distance-time graphs to show:
(a) Increasing velocity
(b) Uniform velocity and
(c) Decreasing velocity

Solution 14

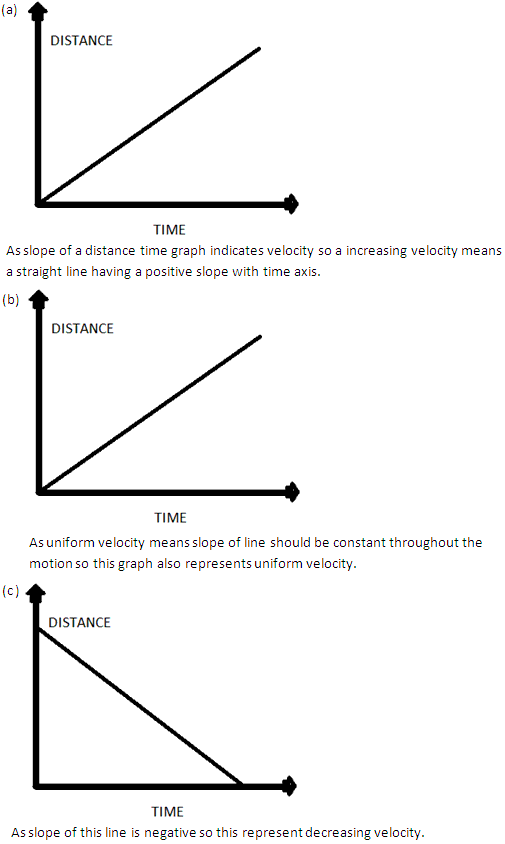
Question 15

Draw velocity-time graph to show:
(a) Acceleration
(b) Deceleration
(c) Zero acceleration
Write a sentence to explain the shape of each graph.

Solution 15

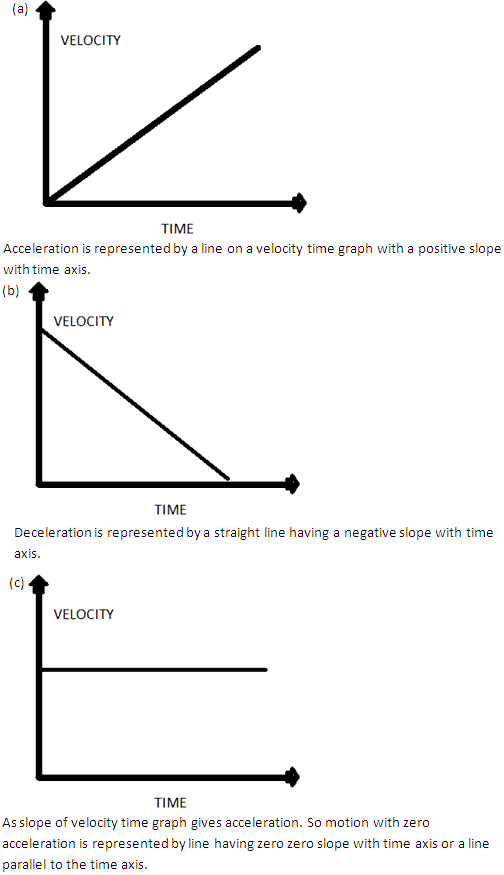
Question 16

Name the physical quantity associated with the rate of change of displacement with time.

Solution 16

Velocity is the physical quantity associated with the rate of change of displacement with time.

Question 17

Define angular velocity.

Solution 17

Question 18

How many types of rectilinear motion are there?

Solution 18

There are three types of rectilinear motion Translational , vibrational and rotational.

Question 19

When a body said to have a uniform velocity?

Solution 19

A body is said to have a uniform velocity if it covers equal displacement in equal interval of time.

Question 20

Out of energy and acceleration, which one is a vector?

Solution 20

Acceleration is a vector quantity.

Question 21

What does the slope of speed-time graph indicate?

Solution 21

Slope of speed time graph represents acceleration.

Question 22

A stone is dropped from a certain height. Is its motion uniform or non-uniform?

Solution 22

If a stone is dropped from a certain height then it undergoes non uniform velocity motion.

Chapter 2 - Motion in One Dimension Exercise 84

Question 1

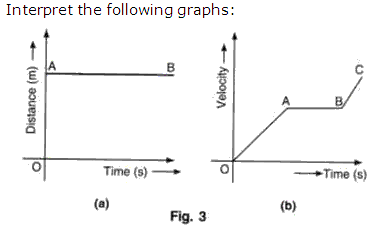
Solution 1

Question 2

During circular motion, which physical quantity of the body,
(a) Remains constant
(b) Changes continuously?

Solution 2

During circular motion
(a) Speed remains constant.
(b) Velocity changes continuously.

Question 3

Is the following statement correct? If not, modify it suitably to make it correct. "The earth moves round the sun with uniform velocity".

Solution 3

The statement is not correct , the correct statement is "the earth is moves round the sun with constant speed".

Question 4

A particle moves along a circular path. How many times does it change its direction in two complete rounds?

Solution 4

As in circular motion direction changes continuously with motion so after two complete revolutions we can say that direction has changed infinite times.

Question 5

A body moves along a circular path of radius r. When it completes three complete rounds, what is the ratio of distance covered to its displacement?

Solution 5

As after completing 3 revolution in circular motion the displacement is = 0. so the ratio of distance covered to the displacement is infinite.

Question 6

What happens to the stepwise increasing speed-time graph when the size of each step is made very small?

Solution 6

The graph becomes straight line with positive slope with time axis and represents almost a constant acceleration.

Question 7

A body has an acceleration of -3.5 ms^-2. What is its retardation?

Solution 7

Retardation is negative of acceleration so retardation the body is +3.4 ms^-2.

Question 8

The average time taken by a normal person to react to an emergency is one fifteenth of a second and is called the 'reaction time'. If a bus is moving with a velocity of 60 km/h and its driver sees a child running across the road, how much distance would the bus had moved before he could press the brakes? The reaction time of the people increases when they are intoxicated. How much distance had the bus moved if the reaction time of the driver were 1/2 s under the influence of alcohol?

Solution 8

Bus is moving with initial velocity of u = 60 km/hr.
60 km/hr = ( 60 X 1000)/3600 = u = 16.66 ms^-1.
Reaction time = t =1/15 sec.
Distance would the bus had moved before pressing the bus would be = u X t.
S = 16.66 X 1/15 = 1.1 m.
Now if the driver is intoxiacated then reaction time would be t = 1/2 seconds.
So S becomes S = u X t = 16.66 X 1/2 = 8.33m.

Question 9

A girl had designed a clap switch for a science exhibition that enabled her to switch on or off an alarm just with clapping of hands. While testing her device in a hall, she noticed that once the alarm has sounded it followed with another one due to echo of the clap, that is, the sound reflected by the walls. She recorded the two soundings of alarm with her tape recorder and found out that time difference in between them is 0.1 s. If the distance of the walls be 15 m, calculate the speed of sound.

Solution 9

Time difference of 0.1 s denotes the time taken by sound to go from device to wall and back to wall. As the distance between wall and device is 15 m so total distance covered by sound is 2 X 15 m =30 m.
So speed of sound is = total distance covered/time taken = 30/0.1 =300 ms^-1.
So speed of sound is 300 ms^-1.

Question 10

An artificial satellite is moving in a circular orbit of radius nearly 42,250 km. Calculate its linear velocity, if it takes 24 hours to revolve round the earth.

Solution 10

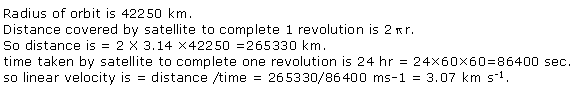
Question 11

Solution 11

Question 12

What does the slope of velocity-time graph represent?

Solution 12

slope of velocity time graph represents acceleration of the body.

Question 13

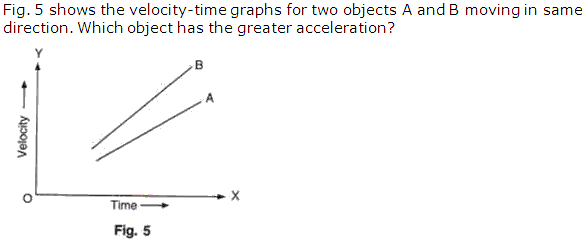
Solution 13

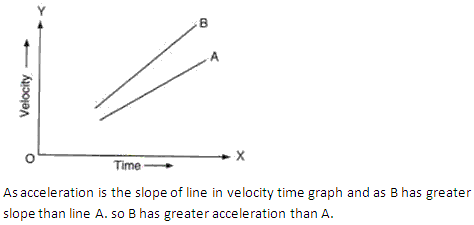
Chapter 2 - Motion in One Dimension Exercise 85

Question 1

Sketch the shape of the velocity-time graph for a body moving with (a) Uniformly velocity, (b) Uniform acceleration.

Solution 1

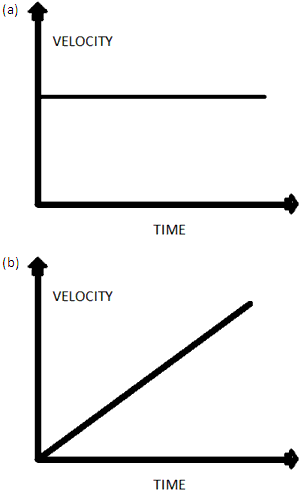
Question 2

Solution 2

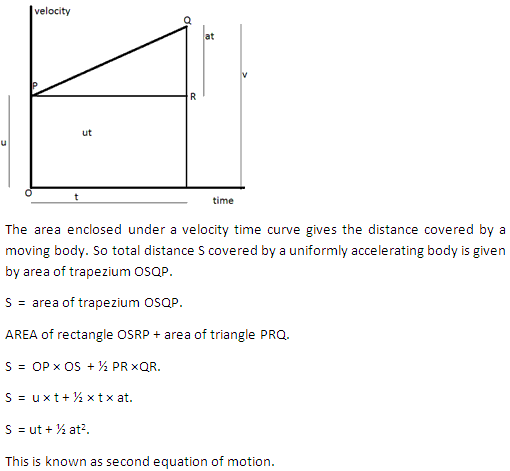
Question 3

Derive the equation
V²-u² = 2as

Solution 3

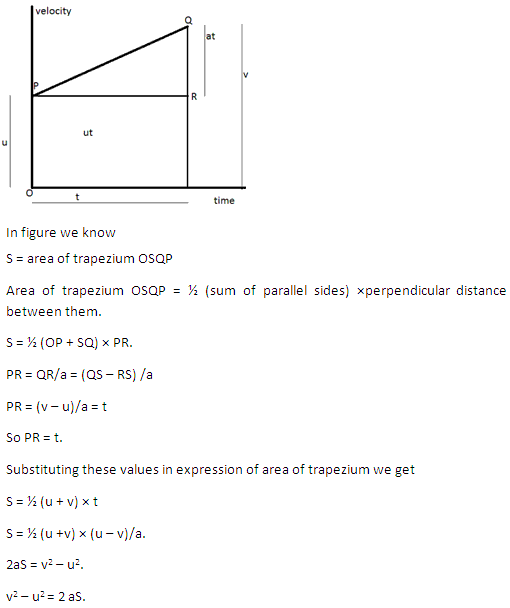
Question 4

For a body moving along a circular path, show that:
Linear speed = Angular velocity X radius of the circle

Solution 4

Question 5

Draw the distance-time graphs of the bodies P and Q starting from rest, moving with uniform speeds with P moving faster than Q.

Solution 5

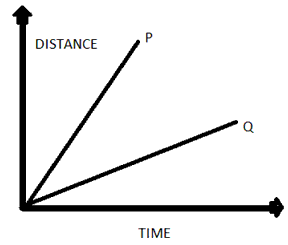
Question 6

A body covers half the distance with the speed A and the other half with speed B. What will be the average speed for the whole journey?

Solution 6

let  total distance be S.
Boy covers distance S/2  with speed  A then time taken by him to cover this distance would be T₁ =S/2A.
Again boy covers rest of the distance S/2 with speed B then time taken by him to cover this distance would be T₂  =S/2B.
So total time taken by boy to cover the distance S is T = T₁ + T₂.
Total time T= S/2 (1/A +1/B) = s(A+B)/2AB.
And average speed  = S/T = 2AB/(A+B).

Question 7

A car travels 30 km at a uniform speed of 60 km/h and the next 30 km at a uniform speed of 20 km/h. What is its average speed?

Solution 7

Car travls 30 km distance with speed 60 km/hr
Time taken by car to travel this distance = 30/60 = 0.5 hr.
Car travels another distance of 30 km with speed of 20 km/hr.
Time taken by car to travel this distance = 30/20 = 1.5 hr.
Total time taken = 1.5 + 0.5 = 2 hr.
Total distance  = 30+ 30 = 60 km.
Average speed of car = 60/2 = 30 km/hr.

Question 8

On a 120 km track, a train travels the first 40 km at a uniform speed of 30 km/h. How fast must the train travel the next 80 km, so as to average 60 km/h for the entire trip.

Solution 8

Train travels first 40 km at speed of 30 km/hr.
Time taken by train to cover this distance is = distance/speed = 40/30 = 4/3 hr.
Let speed of train to cover next 80 km is v .
Then time taken by train to cover these 80 km is 80/v.
Total time becomes T = 4/3 +80/v = ( 4v + 240)/3v.
Total distance= 120 km.
Average speed = 60 km/h (given)
However average is given by = total distance /total time.
So (120 X 3 X v)/(4v +240) = 60
360 v = 240v +14400
120v = 14400
v= 14400/120 =120 km/hr.
so train has to cover those 80 km at a speed of 120 km/hr.

Question 9

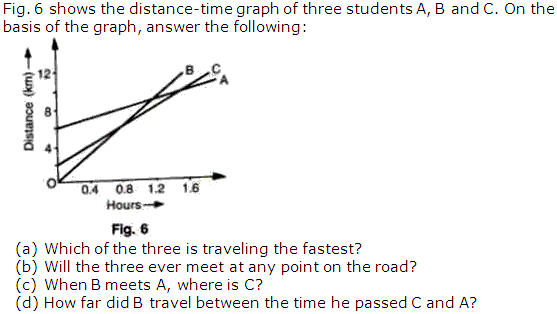
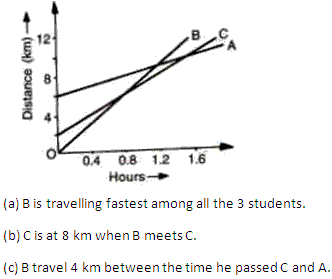
Solution 9

Question 10

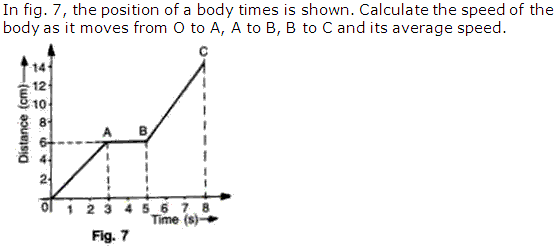
Solution 10

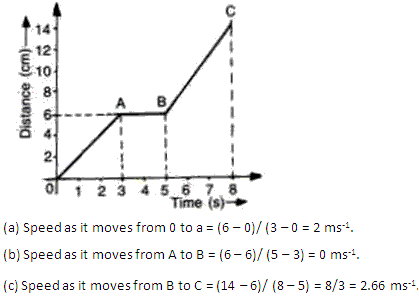
Question 11

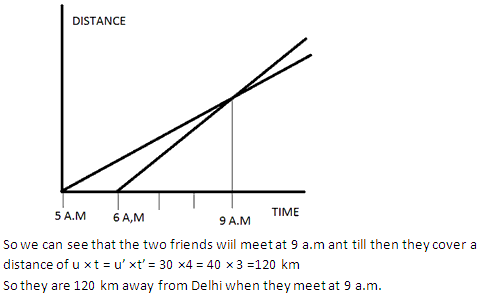
Two friends leave Delhi for Chandigarh in their cars. A  starts at 5 am and moves with a constant speed of 30 km/h, whereas B starts at 6 am and moves with a constant speed of 40 kmh^-1. Plot the distance-time graph for their motion and find at what time the two friends will meet and at what distance from Delhi.

Solution 11

Question 12

A car accelerates uniformly from a velocity of 18 km/h to 36 km/h in 15 min. What is its acceleration?

Solution 12

Initial velocity of car u = 18 km/hr.
Final velocity of car v= 36 km/hr.
Time taken by body = 15 min. = 1/4 hr
Acceleration of car a = ( v- u )/t = (36 - 18 ) X 4 = 72 kmh^-2.

Question 13

A car is moving with a speed of 50 km/h. One second later, its speed is 55 km/h. What is its acceleration?

Solution 13

Initial speed of car u = 50 km/h.
Final speed of car v = 55 km/h.
Time taken by car to attain this speed is = 1 sec. = 1/3600 hr.
Acceleration of the car is = (55 - 50 )X 3600 = 18000 kmh^-2.

Question 14

Convert the following accelerations:
(a) 7200 km/h² into m/s²
(b) 1/36 m/s² into km/h²

Solution 14

(a) 7200 km/h² = ( 7200 X 1000)/(3600 X 3600) = 5/9 ms^-2.
(b) 1/36 m/s² = (1 X3600 X 3600)/(36 X1000) = 3600 kmh^-2.

Question 15

A body moves along a straight road with a speed of 20 m/s and has a uniform acceleration of 5 m/s². What will be its speed after 2 s?

Solution 15

initial velocity u = 20 m/s.
Acceleration = 5 m/s².
T = 2 s.
We know v= u + at.
v= 20 + 5X2= 30 m/s.

Question 16

A car moving with a uniform acceleration of 10 m/s² on a straight road changes its speed from 10 m/s to 30 m/s. Find the time lapsed for the change of speed.

Solution 16

acceleration of the car = 10 ms^-2.
Initial velocity  u = 10 m/s.
Final velocity v = 30 m/s.
We v = u + at.
T = (v- u)/a
T = (30 - 10 )/10 = 2 sec.
Time taken by car is 2 sec.

Chapter 2 - Motion in One Dimension Exercise 86

Question 1

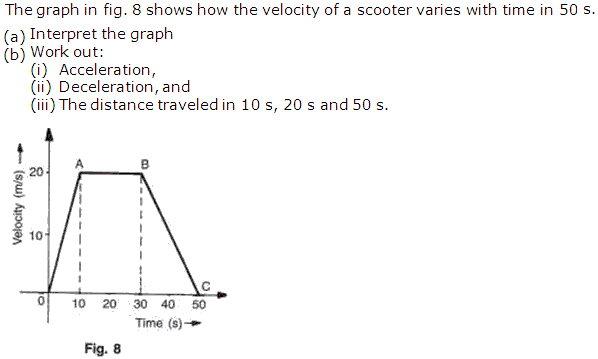
Solution 1

Question 2

A car accelerates to a velocity of 30 m/s in 10 s and then decelerates for 20 s so that it stops. Draw a velocity-time graph to represent the motion and find:
(a) the acceleration,
(b) the deceleration,
(c) the distance travelled.

Solution 2

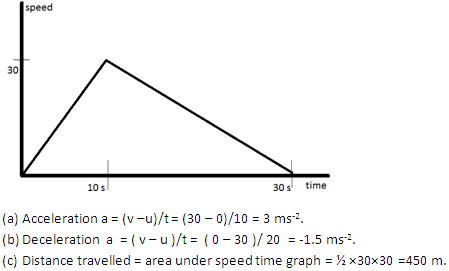
Question 3

A body moves along a straight track. Half of the distance it covers with a velocity of 40 ms^-1 and the remaining half with a velocity of 60 ms^-1. What is the average velocity for the whole journey?

Solution 3

Let total distance be S.
Body covers distance S/2 with speed 40 ms^-1 then time taken by him to cover this distance would be T₁ =S/2 X 40.
Again body covers rest of the distance S/2 with speed 60 ms^-1 then time taken by him to cover this distance would be T₂ =S/2 X 60.
So total time taken by body to cover the distance S is T = T₁ + T₂.
Total time T= S/2 (1/40 +1/60) = s(40+60)/2 X 40 X 60 = s/48.
And average speed = S/T = 48 ms^-1.
So average speed is 48 ms^-1.

Question 4

A body goes from A to B with a velocity of 30 ms^-1 and comes back from B to A with a velocity of 20 ms^-1. What is the average velocity of the body for the whole journey?

Solution 4

As  displacement for the motion from A to B and B to A is zero so the average velocity of the body would be zero.

Question 5

A body starts to slide over a horizontal surface with an initial velocity of 0.5 ms^-1. Due to friction, its velocity decreases at the rate of 0.05 ms^-2. How much time will it take for the body to stop?

Solution 5

Initial velocity of body u = 0.5 ms^-1.
Final velocity of the body v = 0 ms^-1 as body comes to rest finally.
Retardation of body = 0.05 ms^-2.
We know that v = u + at.
0 = 0.5 - 0.05t
T = 0.5/0.05 = 10 sec.

Question 6

A train is moving at a speed of 90 km/h. On applying brakes, a retardation of 2.5 ms^-2 is created. At what distance before, should the driver apply the brakes to stop the train at the station?

Solution 6

Initial speed of train = 90 km/hr
Speed of train imn m/s = ( 90 X 1000 )/3600 = 25 m/s.
Retardation of the train = 2.5 ms^-2.
Final speed of train at platform = 0 m/s.
We know that v2 - u2 = 2as.
0 - 25 X25 = 2 X (-2.5) X s
S = 625/5 = 125 m.
So driver should apply the brakes 125 m before the platform.

Question 7

A 50 m long train passes over a bridge at a speed of 30 km/h. If it takes 36 seconds to cross the bridge, calculate the length of the bridge.

Solution 7

speed of train = 30 km/hr.
Speed in m/s = ( 30 X1000 )/3600 = 50/6 m/s.
Lenth of train = 50 m.
Let lenth of bridge be s metre.
Train has to cover total distance of 50 +s to cross that bridge.
Time taken by train to cover this distance = 36 sec.
So as time taken = total distance /total time taken.
36 = ( 50 +s ) X 6/ 50.
1800 = 300 + 6s
6s = 1500.
S = 1500/6 =  250m
Length of bridge is 250 m.

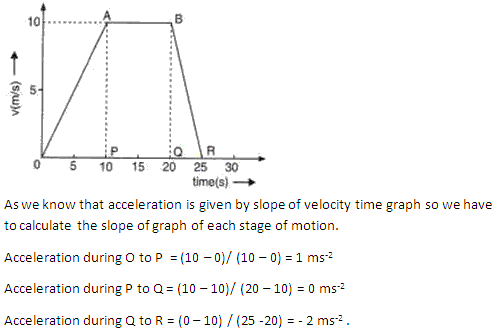
Question 8

Solution 8

Question 9

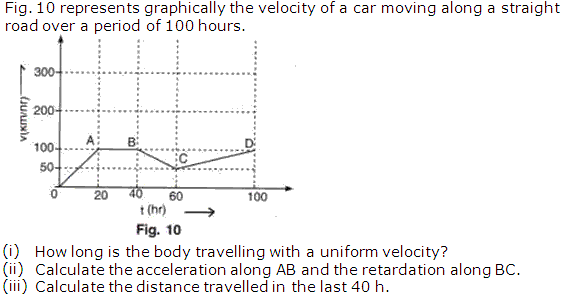
Solution 9

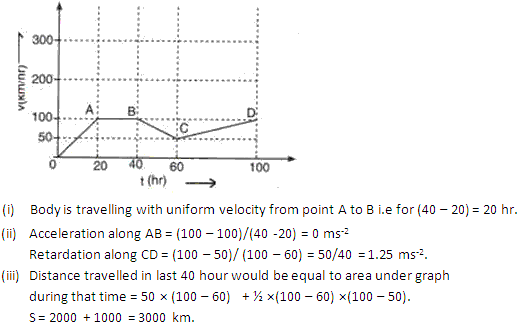
Chapter - Exercise

Solution 1

Chapter 2 - Motion in One Dimension Exercise 87

Question 1

Solution 1

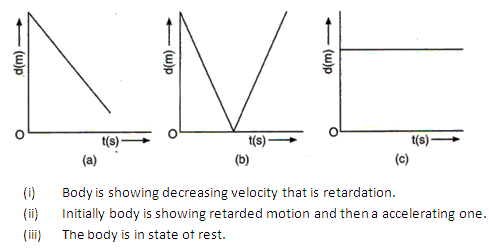
Question 2

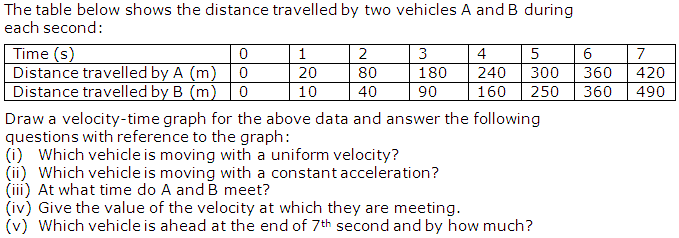
Solution 2

(i) No vehicle is moving with uniform velocity.
(ii) Vehicle B is moving with constant acceleration.
(iii) At 6 seconds both vehicles would meet.
(iv) Velocity of both the vehicles is 60 m/s when they meet.
(v) Vehicle B is ahead at the end of 7^th sec and by 70 m.

Question 3

Solution 3

The given question is wrong as distance can never DECREASE with progress of time.