FRANK Solutions for Class 9 Maths Chapter 15 - Mid-point and Intercept Theorems

FRANK Solutions for Class 9 Maths Chapter 15 - Mid-point and Intercept Theorems

Chapter 15 - Mid-point and Intercept Theorems Exercise Ex. 15.1

Question 1

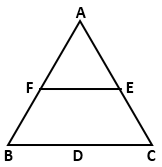
InABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm

Solution 1

Question 2

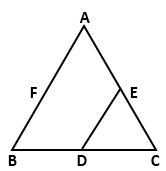
InABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm

Solution 2

Question 3

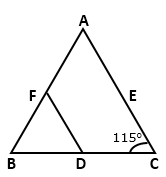
InABC, D, E, F are the midpoints of BC, CA and AB respectively. Find

FDB ifACB = 115°.

Solution 3

Question 4

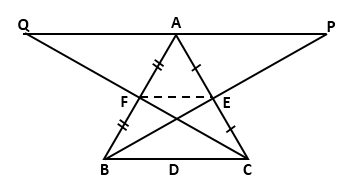
InABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that:

a) QAP is a straight line.

b) A is the mid-point of PQ

Solution 4

Question 5

In a right-angled triangle ABC. 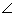ABC = 90° and D is the midpoint of AC. Prove that BD =AC.

Solution 5

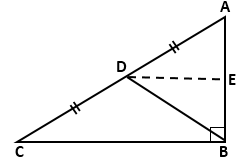
Question 6

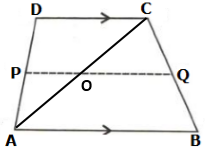
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find:

a) PQ, if AB = 12 cm and DC = 10 cm.

b) AB, if DC = 8 cm and PQ = 9.5 cm

c) DC, if AB = 20 cm and PQ = 14 cm 

Solution 6

Let us draw a diagonal AC which meets PQ at O as shown below:

Question 7

AD is a median of side BC ofABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF : AC = 1 : 3.

Solution 7

Construction: Draw DS ∥ BF, meeting AC at S.

Question 8

InABC, D, E and F are the midpoints of AB, BC and AC.

a. Show that AE and DF bisect each other.

b. If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.

Solution 8

Question 9

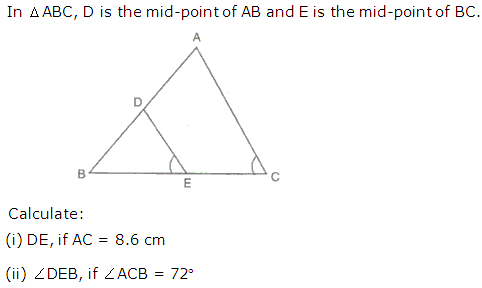
Solution 9

Question 10

Solution 10

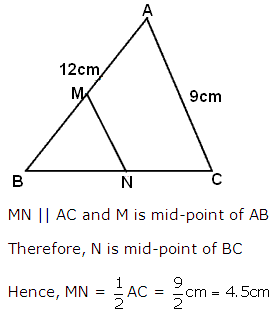
Question 11

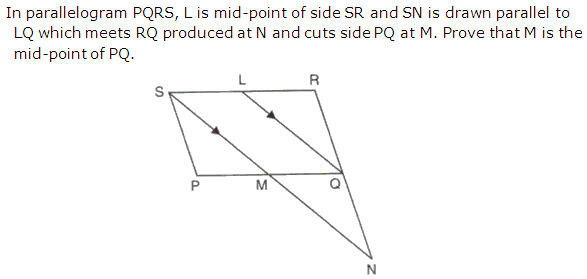
Solution 11

Question 12

Solution 12

Question 13

Solution 13

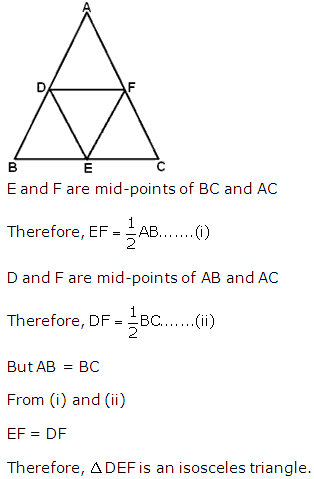
Question 14

Solution 14

Question 15

Solution 15

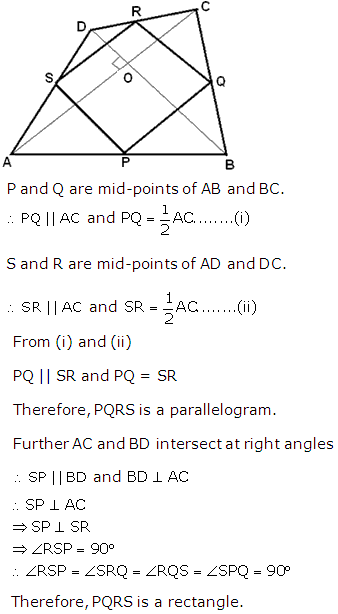
Question 16

Solution 16

Question 17

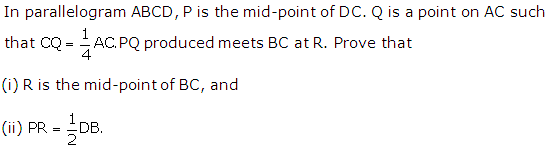
Solution 17

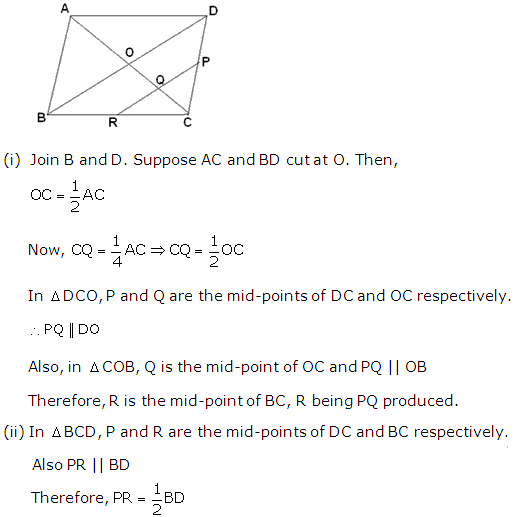
Question 18

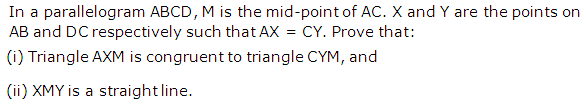
Solution 18

Question 19

Solution 19

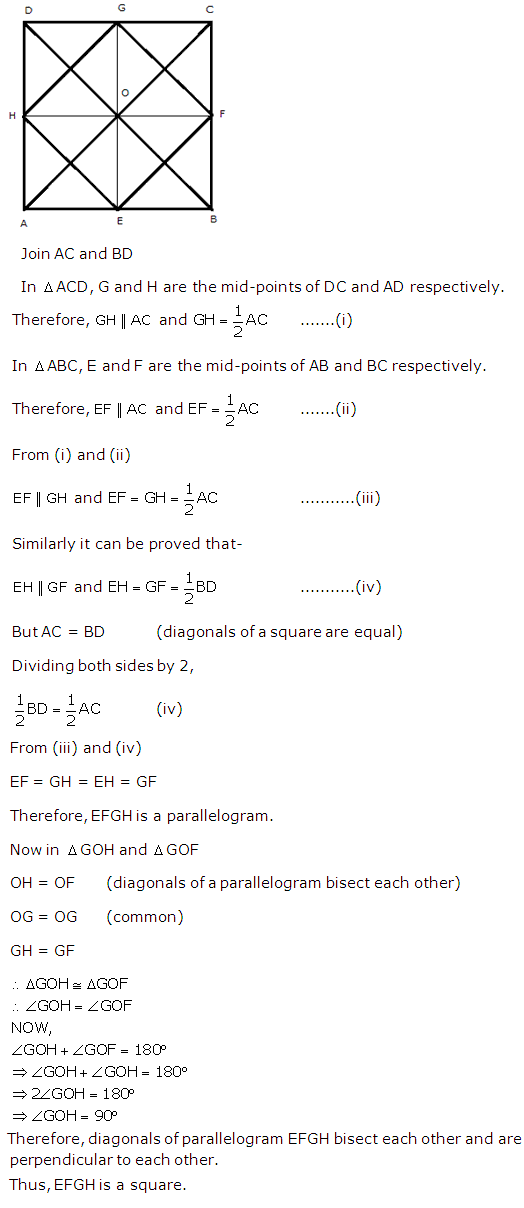
Question 20

Solution 20

Question 21

Solution 21

Question 22

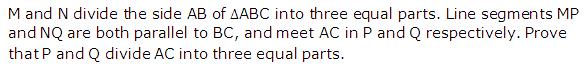
Solution 22

Question 23

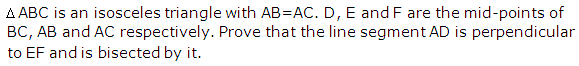
Solution 23

Question 24

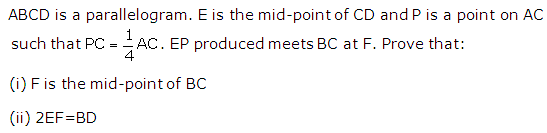
Solution 24

Question 25

Solution 25

Question 26

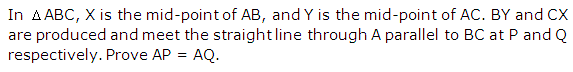
Solution 26

Chapter 15 - Mid-point and Intercept Theorems Exercise Ex. 15.2

Question 1

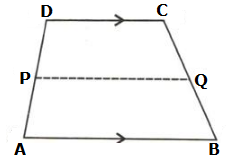
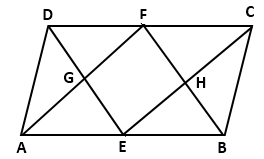
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that:

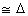a. GEA GFD

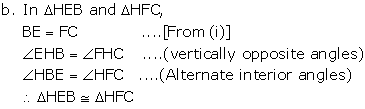
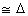b. HEB HFC

c. EGFH is a parallelogram

Solution 1

Question 2

InABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that:

a. Q A and P are collinear.

b. A is the mid-point of PQ

Solution 2

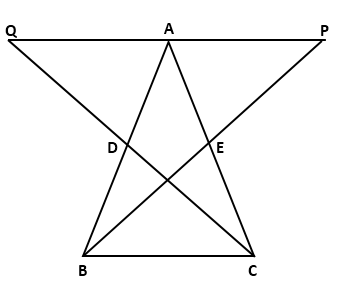
Question 3

In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.

 

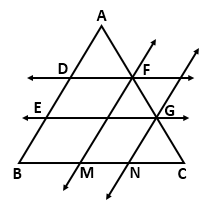
Solution 3

Question 4

In the given figure, the lines l, m and n are parallel to each other. D is the midpoint of CE. Find:

a. BC, b. EF, c. CG and d. BD.

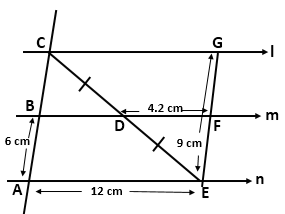
Solution 4

Question 5

The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.

Solution 5

The figure is as below:

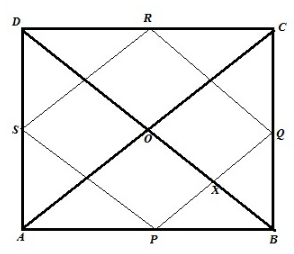
Let ABCD be a quadrilateral where P, Q, R, S are the midpoints of sides AB, BC, CD, DA respectively.

Diagonals AC and BD intersect at right angles at point O. We need to show that PQRS is a rectangle

Question 6

InABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.

Solution 6

Note: This question is incomplete.

According to the information given in the question,

F could be any point on BC as shown below:

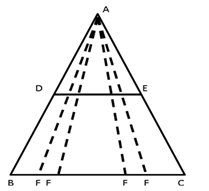
So, this makes it impossible to prove that DP = DE, since P too would shift as F shift because P too would be any point on DE as F is.

Note: If we are given F to be the mid-point of BC, the result can be proved.

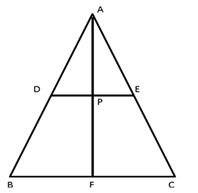
Question 7

InABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.

Remark: Figure is incorrect in Question

Solution 7

From the figure EF ∥ AB and E is the midpoint of BC. 

Therefore, F is the midpoint of AC. 

Here EF ∥ BD, EF = BD as D is the midpoint of AB. 

BE ∥ DF, BE = DF as E is the midpoint of BC. 

Therefore BEFD is a parallelogram.

Remark: Figure modified

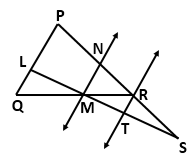
Question 8

In the given figure, PS = 2RS. M is the midpoint of QR. If TR ∥ MN ∥ QP, then prove that:

 

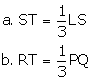
Solution 8

Question 9

In the given figure, T is the midpoint of QR. Side PR ofPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR =PQ.

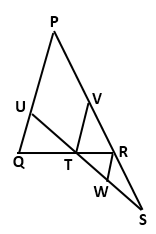
Solution 9