FRANK Solutions for Class 9 Maths Chapter 8 - Simultaneous Linear Equations
Chapter 8 - Simultaneous Linear Equations Exercise Ex. 8.1
Question 1
Solve the following simultaneous equations by the
substitution method:
2x + y = 8
3y = 3 + 4x
Solution 1
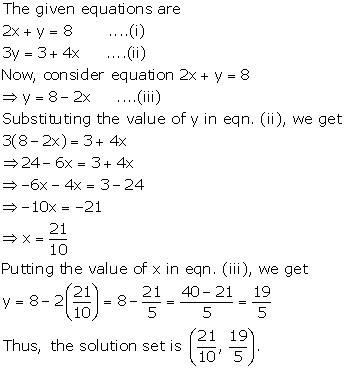
Question 2
Solve the following simultaneous equations by the
substitution method:
x + 3y= 5
7x - 8y = 6
Solution 2
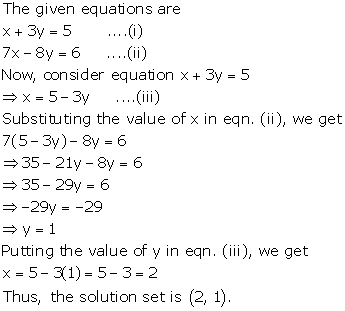
Question 3
Solve the following simultaneous equations by the
substitution method:
5x + 4y - 23 = 0
x + 9 = 6y
Solution 3
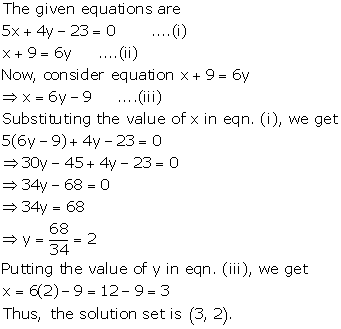
Question 4
Solve the following simultaneous equations by the substitution
method:
2x + 3y = 31
5x - 4 = 3y
Solution 4
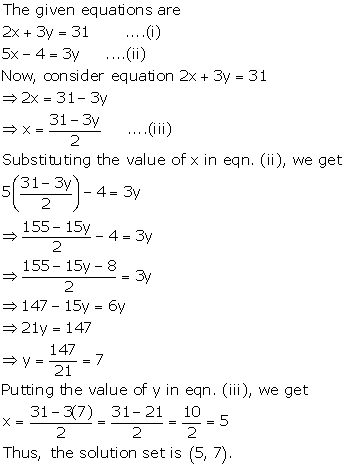
Question 5
Solve the following simultaneous equations by the
substitution method:
7x - 3y = 31
9x - 5y = 41
Solution 5
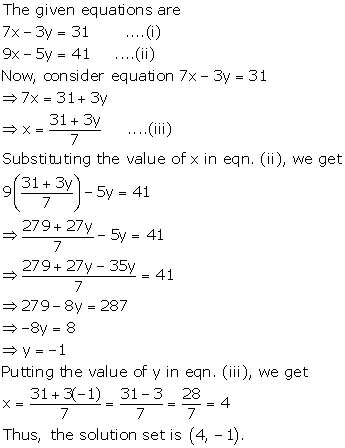
Question 6
Solve the following simultaneous equations by the
substitution method:
13 + 2y = 9x
3y = 7x
Solution 6
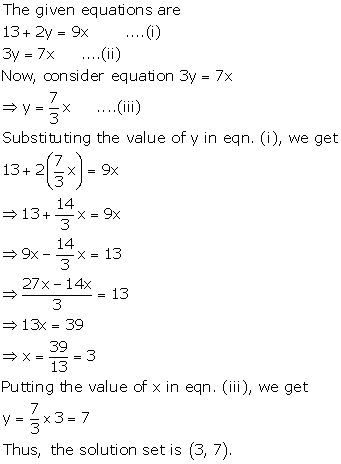
Question 7
Solve the following simultaneous equations by the
substitution method:
0.5x + 0.7y = 0.74
0.3x + 0.5y = 0.5
Solution 7

Question 8
Solve the following simultaneous equations by the
substitution method:
0.4x + 0.3y = 1.7
0.7x - 0.2y = 0.8
Solution 8
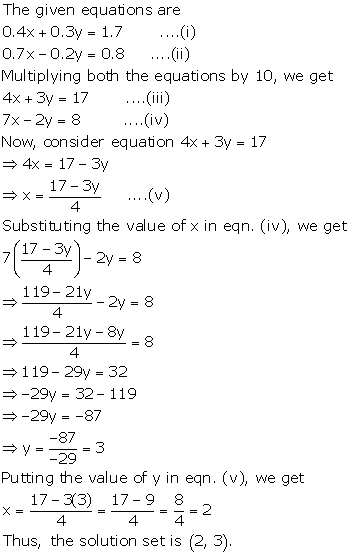
Question 9
Solve the following simultaneous equations by the
substitution method:
3 - (x + 5) = y + 2
2(x + y) = 10 + 2y
Solution 9

Question 10
Solve the following simultaneous equations by the
substitution method:
7(y + 3) - 2(x + 2) = 14
4(y - 2) + 3(x - 3) = 2
Solution 10
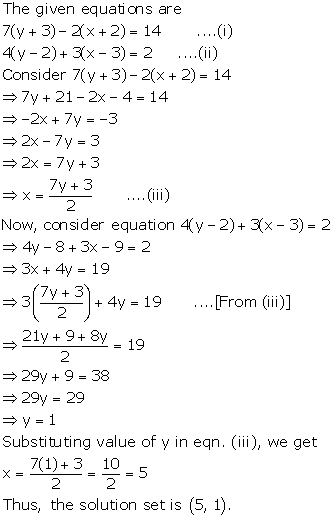
Question 11
Solve the following simultaneous equations:
13a - 11b = 70
11a - 13b = 74
Solution 11
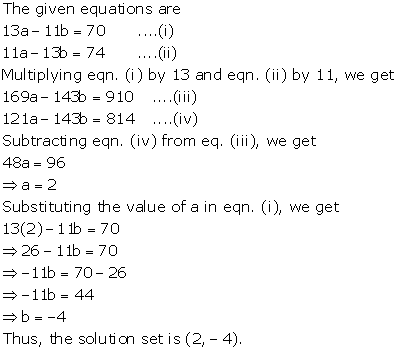
Question 12
Solve the following simultaneous equations:
41x + 53y = 135
53x + 41y = 147
Solution 12
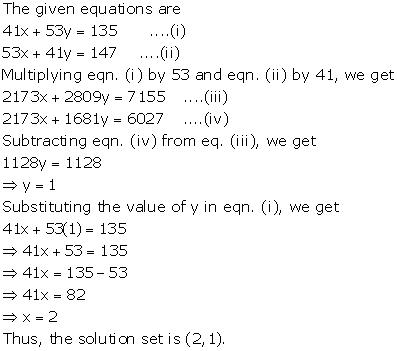
Question 13
Solve the following simultaneous equations:
65x - 33y = 97
33x - 65y = 1
Solution 13
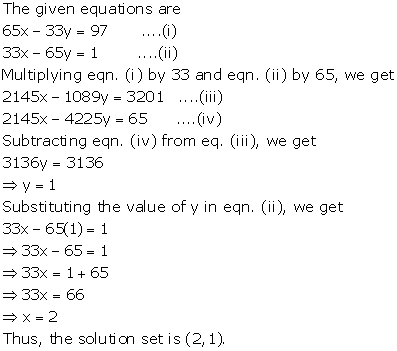
Question 14
Solve the following simultaneous equations:
103a + 51b = 617
97a + 49b = 583
Solution 14

Question 15
Solve the following pairs of equations:
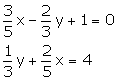
Solution 15
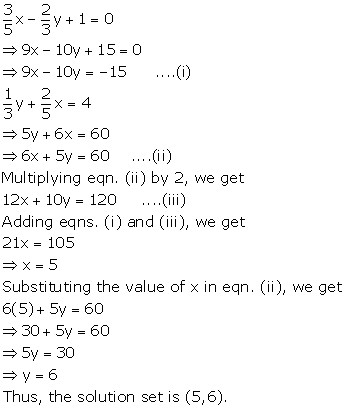
Question 16
Solve the following pairs of equations:
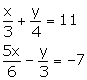
Solution 16

Question 17
Solve the following pairs of equations:
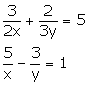
Solution 17

Question 18
Solve the following pairs of equations:
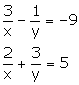
Solution 18

Question 19
Solve the following pairs of equations:
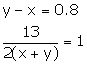
Solution 19
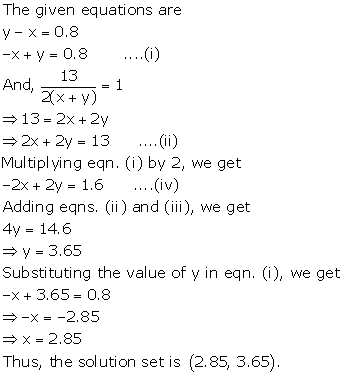
Question 20
Solve the following pairs of equations:
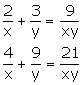
Where x ≠ 0, y ≠ 0
Solution 20
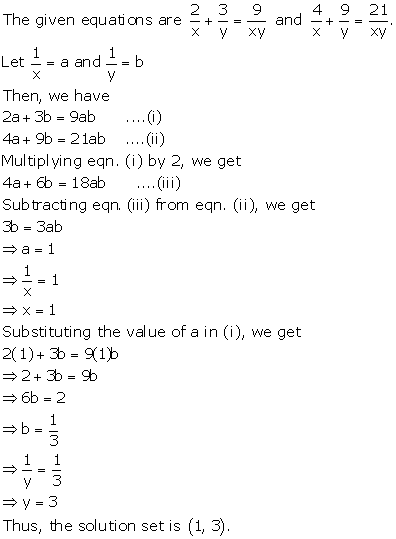
Question 21
Solve the following pairs of equations:
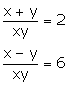
Solution 21
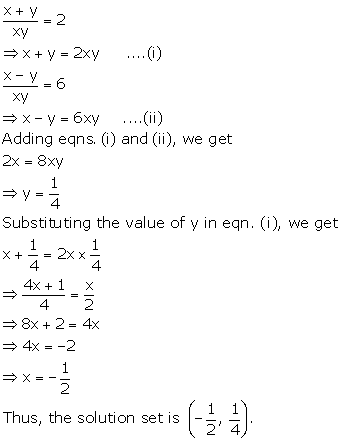
Question 22
Solve the following pairs of equations:
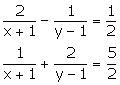
Solution 22
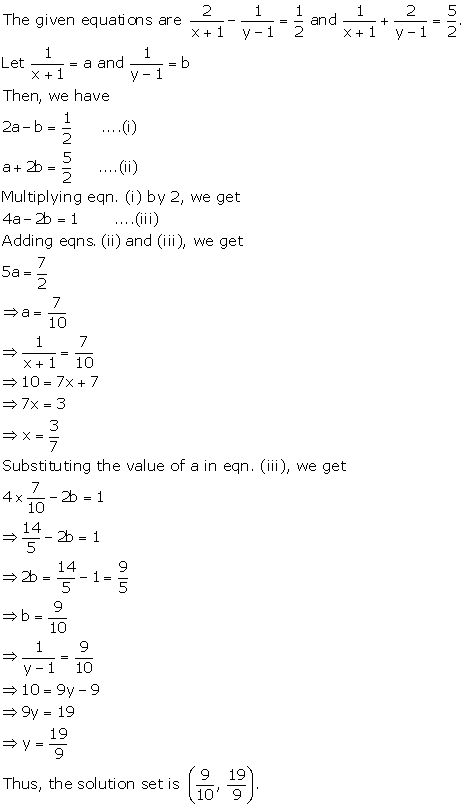
Question 23
Solve the following pairs of equations:
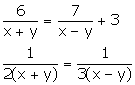
Where x + y ≠ 0 and x - y ≠ 0
Solution 23
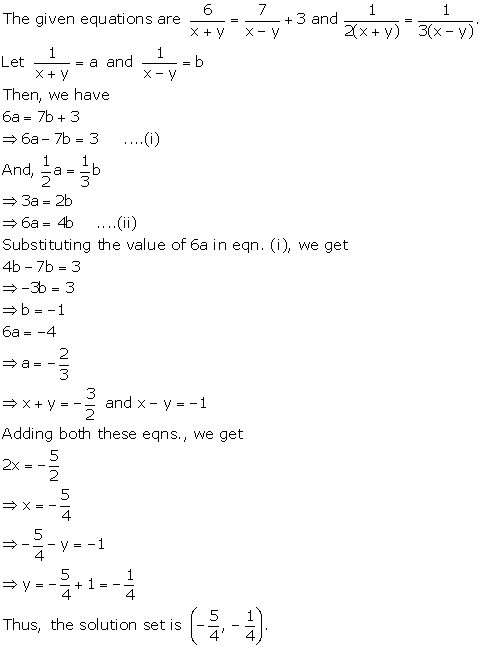
Question 24
Solve the following pairs of equations:
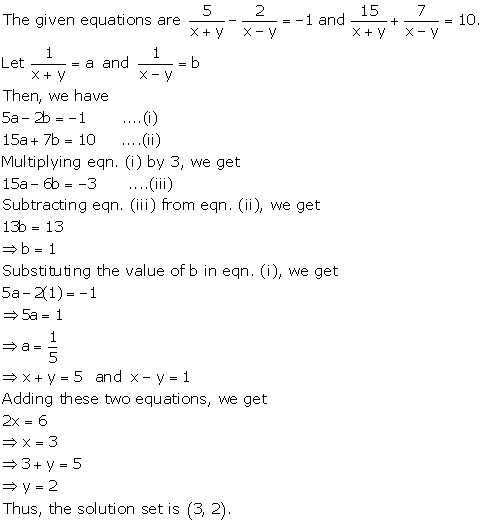
Solution 24
Question 25
Solve the following pairs of equations:
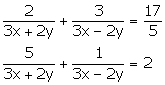
Solution 25
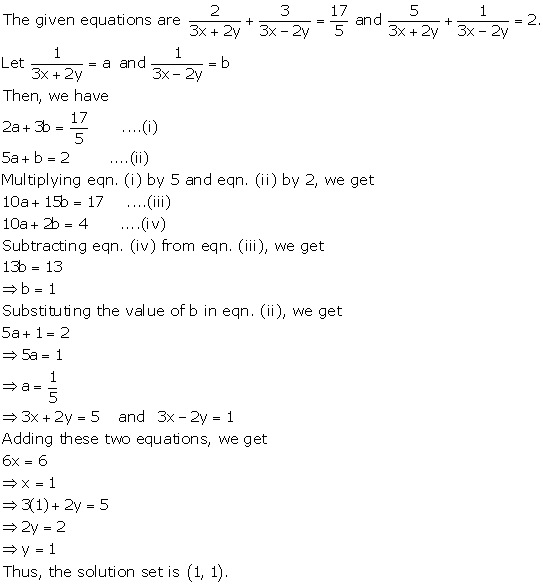
Question 26
Solve the following pairs of equations:
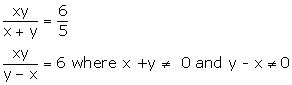
Solution 26
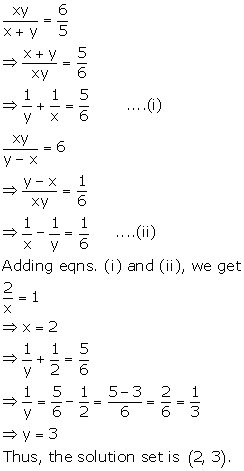
Question 27
Can the following equations hold simultaneously?
7y - 3x = 7
5y - 11x = 87
5x + 4y = 43
If yes, find the value of x and y.
Solution 27
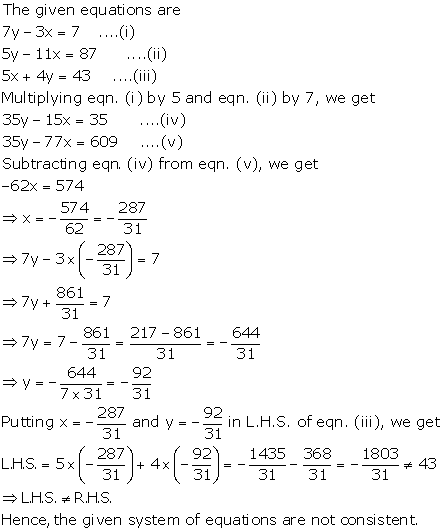
Question 28
If the following three equations hold simultaneously for x
and y, find the value of 'm'.
2x + 3y + 6 = 0
4x - 3y - 8 = 0
x + my - 1 = 0
Solution 28
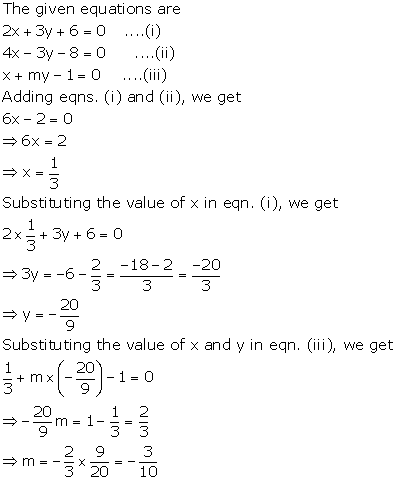
Question 29
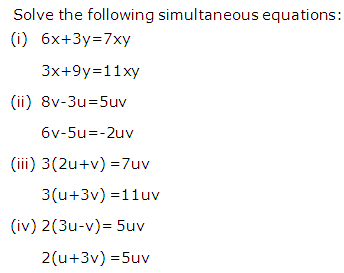
Solution 29
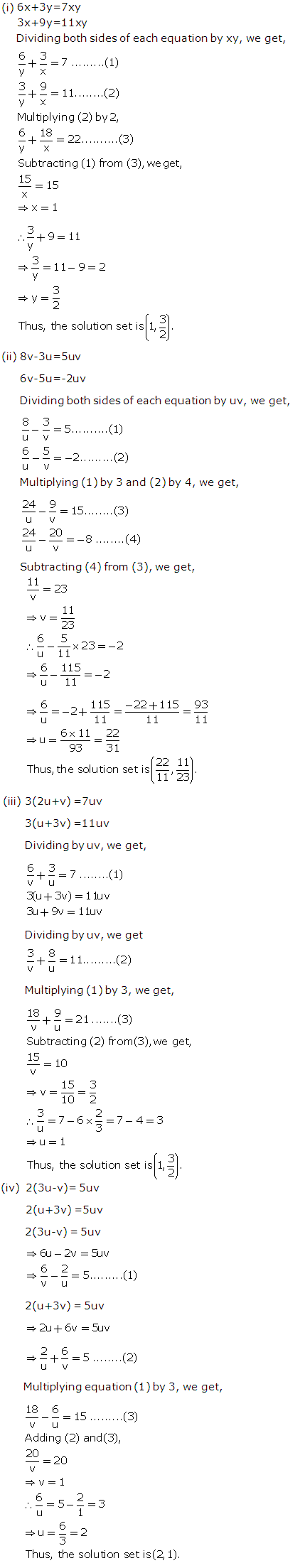
Question 30
Solution 30
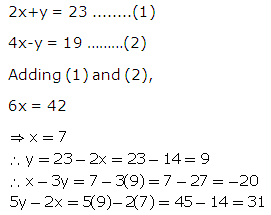
Question 31
Solution 31
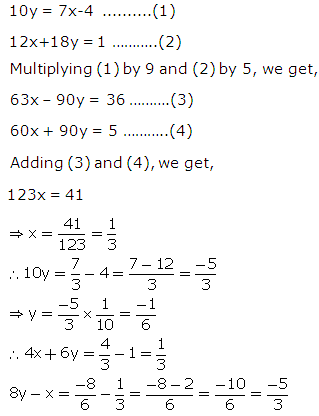
Question 32
Solution 32
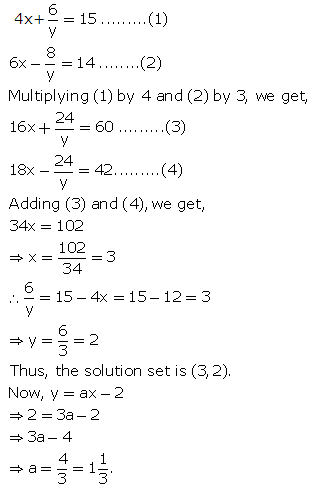
Question 33
Solution 33
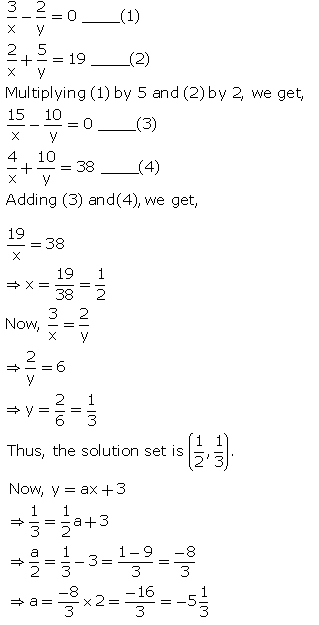
Chapter 8 - Simultaneous Linear Equations Exercise Ex. 8.2
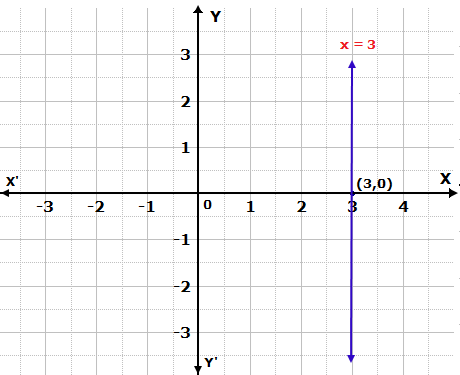
Question 1
Draw the graphs of the following linear equations:
x = 3
Solution 1
The graph of x = 3 is as follows:
Question 2
Draw the graphs of the following linear equations:
y + 5 = 0
Solution 2
Given equation, y + 5 = 0
i.e. y = -5
The graph is as follows:
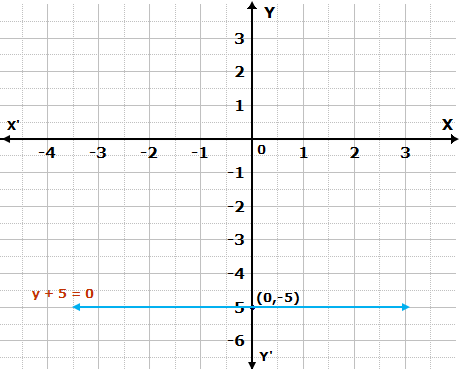
Question 3
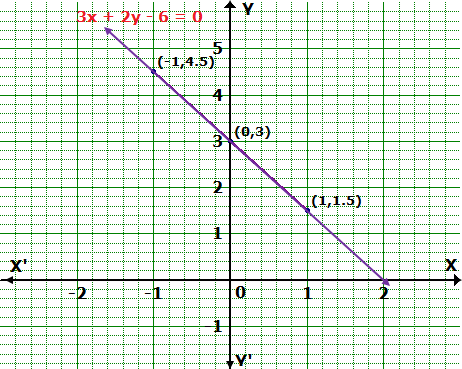
Draw the graphs of the following linear equations:
3x + 2y - 6 = 0
Solution 3

Question 4
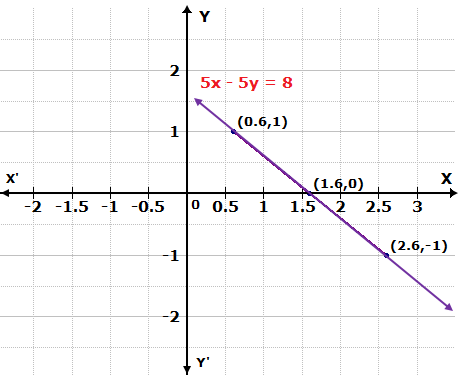
Draw the graphs of the following linear equations:
5x - 5y = 8
Solution 4

Question 5
Draw the graph for each of the following equation: Also,
find the coordinates of the points where the graph of the equation meets the
coordinate axes:
Solution 5

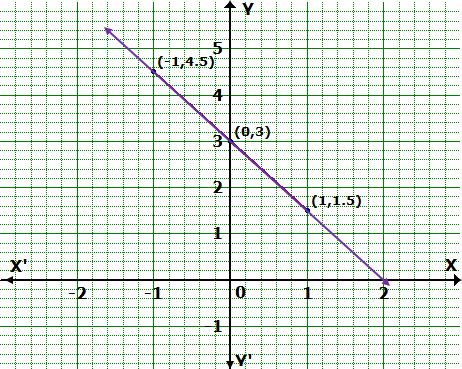
Thus, the graph of the equation meets the X-axis at (2, 0) and Y-axis
at (0, 3).
Question 6
Draw the graph for each of the following equation: Also,
find the coordinates of the points where the graph of the equation meets the
coordinate axes:
Solution 6
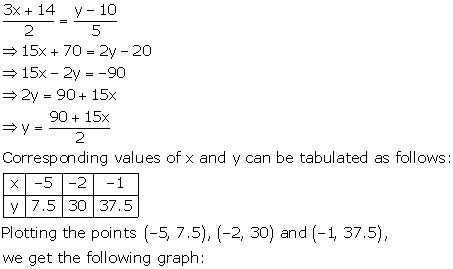
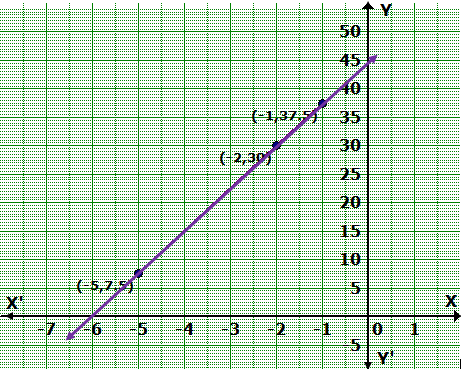
Thus, the graph of the equation meets the X-axis at (-6, 0) and
Y-axis at (0, 45).
Question 7
Draw the graph of the equation 4x - 3y + 12 = 0.
Also, find the area of the triangle formed by the line
drawn and the coordinate axes.
Solution 7

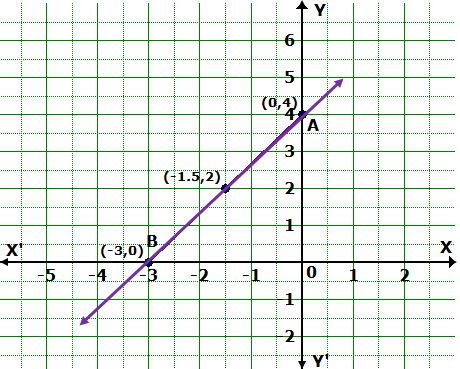
Question 8
Draw the graph of the equation
y = 5x - 4 Find graphically
a. the value of x, when y = 1
b. the value of y, when x = -2
Solution 8
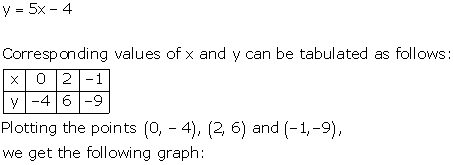
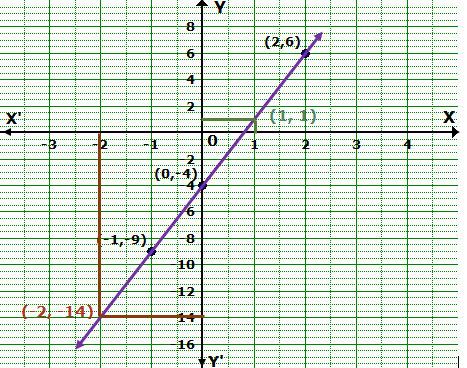
From the graph, we find that
a. When y = 1, x = 1.
b. When x = -2, y = -14
Question 9
Use the given table and draw the graph of a straight line.
x
|
1
|
2
|
3
|
P
|
y
|
1
|
q
|
-5
|
7
|
Find graphically the values of 'p' and 'q'.
Solution 9
The graph is as follows:
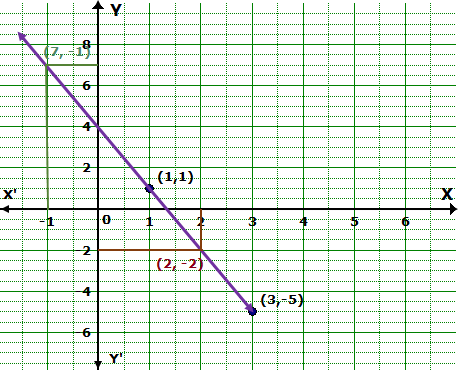
From the graph, we find that p = -1 and q = -2.
Question 10
A straight line passes through the points (2, 5) and (-4,
-7). Plot these points on a graph paper and draw the straight line passes
through these points. If points (a, -1) and (-5, b) lie on the line drawn,
find the value of a and b.
Solution 10
The graph is as follows:
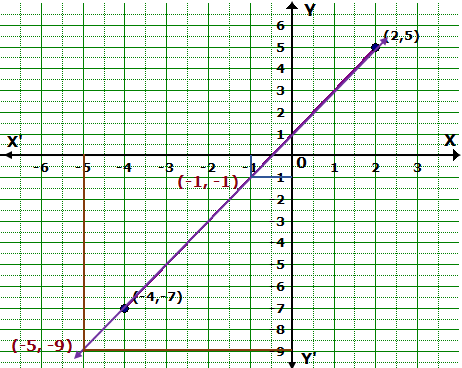
From the graph, we find that a = -1 and b = -9.
Question 11
Solve the following system of equations graphically:
2x = 23 - 3y
5x = 20 + 8y
Also, find the area of the triangle formed by these lines
and x-axis in each graph.
Solution 11

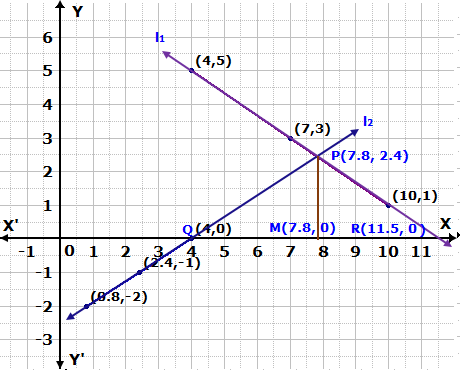

Question 12
Solve the following system of equations graphically:
6x - 3y + 2 = 7x + 1
5x + 1 = 4x - y + 2
Also, find the area of the triangle formed by these lines
and x-axis in each graph.
Solution 12

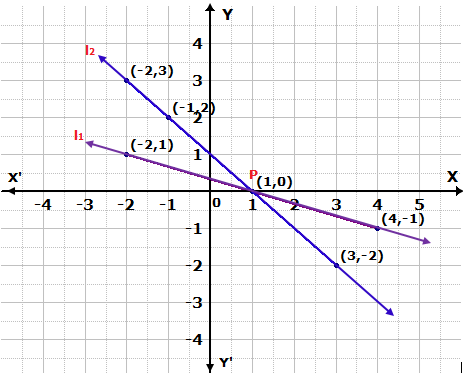

Question 13
Solution 13

Question 14
Solution 14
Question 15
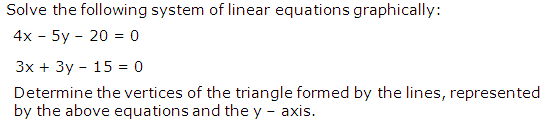
Solution 15
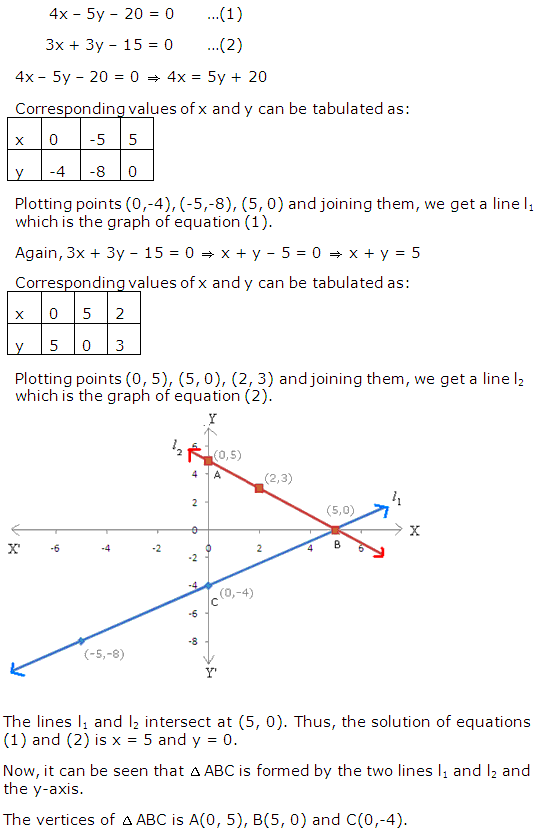
Question 16

Solution 16
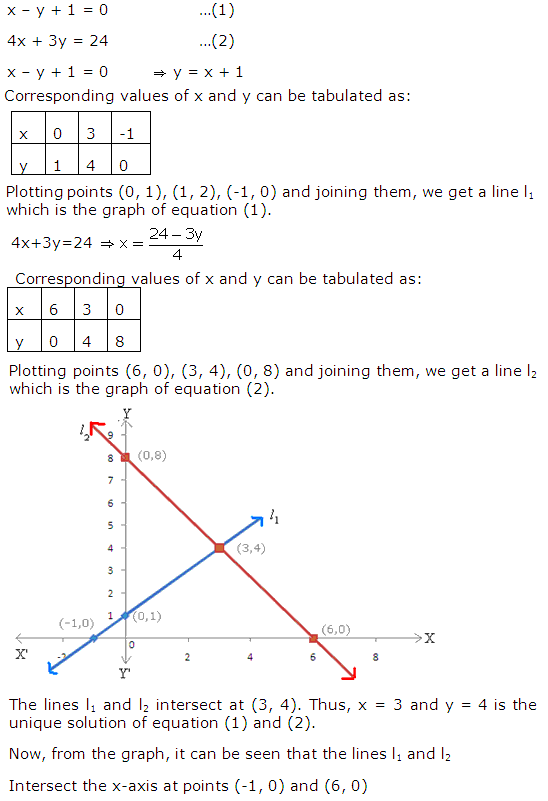
Question 17

Solution 17
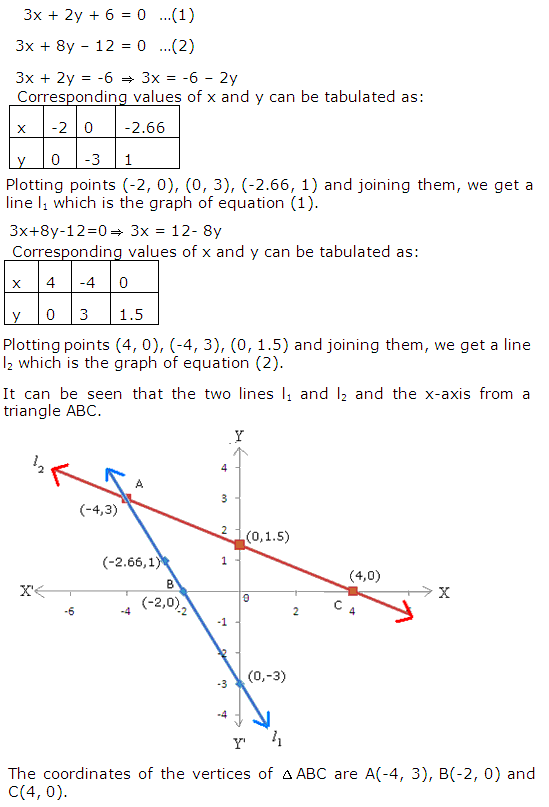
Chapter 8 - Simultaneous Linear Equations Exercise Ex. 8.3
Question 1
The length of a rectangle is twice its width. If its
perimeter is 30 units, find its dimensions.
Solution 1

Question 2
The difference of two numbers is 3, and the sum of three
times the larger one and twice the smaller one is 19. Find the two numbers.
Solution 2

Question 3
If a number is thrice the other and their sum is 68, find
the numbers.
Solution 3
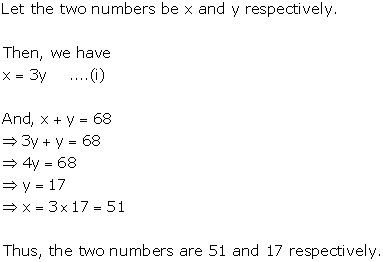
Question 4
The sum of four times the first number and three times the
second number is 15. The difference of three times the first number and twice
the second number is 7. Find the numbers.
Solution 4

Question 5
In a two-digit number, the sum of the digits is 7. The
difference of the number obtained by reversing the digits and the number
itself is 9. Find the number.
Solution 5

Question 6
The sum of a two-digit number and the number obtained by
reversing the digits is 110 and the difference of two digits is 2. Find the
number.
Solution 6

Question 7
Seven more than a 2-digit number is equal to two less than
the number obtained by reversing the digits. The sum of the digits is 5. Find
the number.
Solution 7

Question 8
If
2 is added to the numerator and denominator it becomes 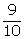 and if 3 is
subtracted from the numerator and denominator it becomes
and if 3 is
subtracted from the numerator and denominator it becomes 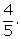 Find the fraction.
Find the fraction.
Solution 8

Question 9
The ratio of two numbers is 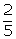 . If 4 is added in first and 32 is subtracted from the
second, the ratio becomes the reciprocal of the original ratio. Find the
numbers.
. If 4 is added in first and 32 is subtracted from the
second, the ratio becomes the reciprocal of the original ratio. Find the
numbers.
Solution 9

Question 10
The sum of the numerator and denominator of a fraction is
12. If the denominator is increased by 3, the fraction becomes 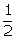 . Find the fraction.
. Find the fraction.
Solution 10

Question 11
If
1 is added to the denominator of a fraction, the fraction becomes 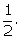 If 1 is added to the numerator of the fraction, the
fraction becomes 1. Find the fraction.
If 1 is added to the numerator of the fraction, the
fraction becomes 1. Find the fraction.
Solution 11

Question 12
The age of the father is seven times the age of the son.
Ten years later, the age of the father will be thrice the age of the son.
Find their present ages.
Solution 12

Question 13
The present ages of Kapil and Karuna are in the ratio 2 :
3. Six years later, the ratio will be 5 : 7. Find their present ages.
Solution 13

Question 14
A father's age is three times the age of his child. After
12 years, twice the age of father will be 36 more than thrice the age of his
child. Find his present age.
*
Question modified
Solution 14

* Question modified
Question 15
In a triangle, the sum of two angles is equal to the third
angle. If the difference between these two angles is 20°, determine all the
angles.
Solution 15

Question 16
In a ABC, ∠A
= x°, ∠B
= (2x - 30)°, ∠C
= y° and also, ∠A
+ ∠B
= one right angle. Find the angles. Also, state the type of this triangle.
Solution 16
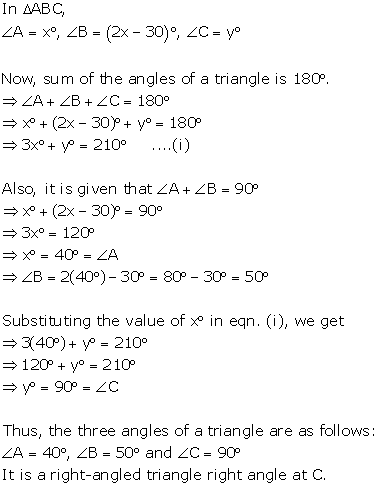
Question 17
A two-digit number is such that the ten's digit exceeds
thrice the unit's digit by 3 and the number obtained by interchanging the
digits is 2 more than twice the sum of the digits. Find the number.
Solution 17

Question 18
Anil and Sunita have incomes in the ratio 3 : 5. If they
spend in the ratio 1 : 3, each saves T 5000. Find the income of each.
Solution 18

Question 19
The ratio of passed and failed students in an examination
was 3 : 1. Had 30 less appeared and 10 less failed, the ratio of passes to
failures would have been 13 : 4. Find the number of students who appeared for
the examination.
Solution 19

Question 20
An eraser costs Rs. 1.50 less than a sharpener. Also,
the cost of 4 erasers and 3 sharpeners is Rs.29. Taking x and y as the costs (in
Rs.) of an
eraser and a sharpener respectively, write two equations for the above
statements and find the value of x and y.
Solution 20

Question 21
A person goes 8 km downstream in 40 minutes and returns in
1 hour. Determine the speed of the person in still water and the speed of the
stream.
Solution 21

Question 22
A boat goes 18 km upstream in 3 hours and 24 km downstream
in 2 hours. Find the speed of the boat in still water and the speed of the
stream.
Solution 22

Question 23
Salman and Kirti start at the same time from two places 28
km apart. If they walk in the same direction, Salman overtakes Kirti in 28
hours but if they walk in the opposite directions, they meet in 4 hours. Find
their speeds (in km/h).
Solution 23

Question 24
A solution containing 12% alcohol is to be mixed with a
solution containing 4% alcohol to make 20 gallons of solution containing 9%
alcohol. How much of each solution should be used?
Solution 24
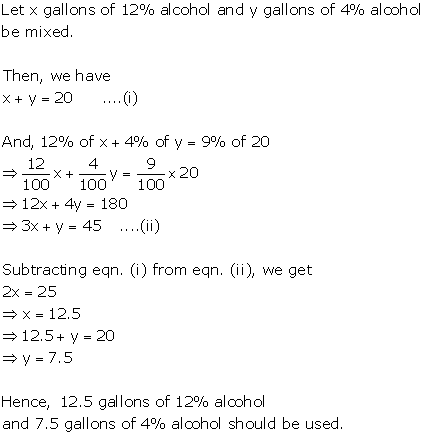
Question 25
9 pens and 5 pencils cost Rs.32, and 7 pens and 8 pencils cost Rs.29. Find the unit
price for each pen and pencil.
Solution 25

Question 26
Sunil and Kafeel both have some oranges. If Sunil gives 2
oranges to Kafeel, then Kafeel will have thrice as many as Sunil. And if
Kafeel gives 2 oranges to Sunil, then they will have the same numbers of
oranges. How many oranges does each have?
Solution 26

Question 27
Samidha and Shreya have pocket money Rs.x and Rs.y respectively at
the beginning of a week. They both spend money throughout the week. At the
end of the week, Samidha spends Rs.500 and is left with as much money as Shreya had in the
beginning of the week. Shreya spends Rs.500 and is left with 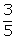 of what Samidha had in the beginning of the week. Find
their pocket money.
of what Samidha had in the beginning of the week. Find
their pocket money.
Solution 27

Question 28
Two mobiles S1 and S2 are sold for Rs. 10,490 making 4%
profit on S1 and 6% on S2. If the two mobiles are sold for Rs.10,510, a profit of 6% is made on S1
and 4% on S2. Find the cost price of both the mobiles.
Solution 28

Question 29
A
and B can build a wall in 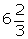 days. If A's one day work is
days. If A's one day work is 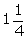 of one day work of B, find in 4 how many days A and B alone
can build the wall.
of one day work of B, find in 4 how many days A and B alone
can build the wall.
Solution 29
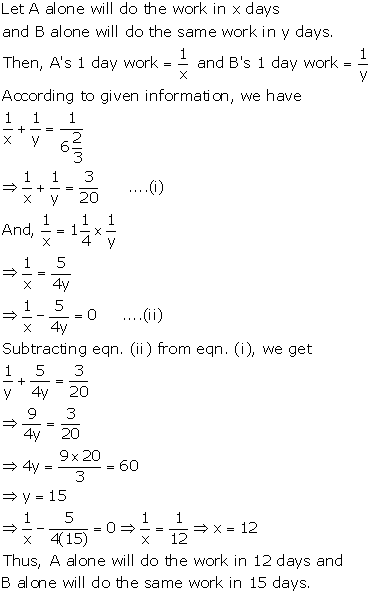

0 comments:
Post a Comment