FRANK Solutions for Class 9 Maths Chapter 13 - Inequalities in Triangles

FRANK Solutions for Class 9 Maths Chapter 13 - Inequalities in Triangles

Chapter 13 - Inequalities in Triangles Exercise Ex. 13.1

Question 1

Name the greatest and the smallest sides in the following triangles:

ABC, ∠ = 56^o, ∠B = 64^o and ∠C = 60^o.

Solution 1

 

Question 2

Name the greatest and the smallest sides in the following triangles:

DEF, ∠D = 32^o, ∠E = 56^o and ∠F = 92^o.

Solution 2

Question 3

Name the greatest and the smallest sides in the following triangles:

XYZ, ∠X = 76^o, ∠Y = 84^o.

Solution 3

 

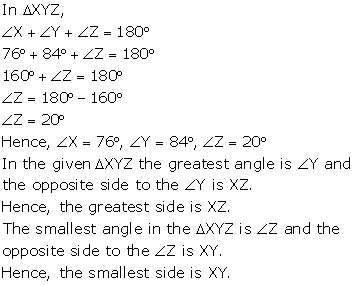
Question 4

Arrange the sides of the following triangles in an ascending order:

ABC, ∠A = 45^o, ∠B = 65^o.

Solution 4

Question 5

Arrange the sides of the following triangles in an ascending order:

DEF, ∠D = 38^o, ∠E = 58^o.

Solution 5

Question 6

In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?

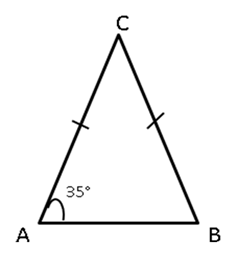
Solution 6

 

Question 7

n the given figure, ∠QPR = 50^o and ∠PQR = 60^o. Show that :

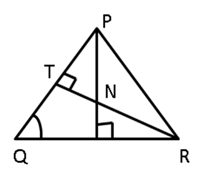
a. PN < RN

b. SN < SR

Solution 7

 

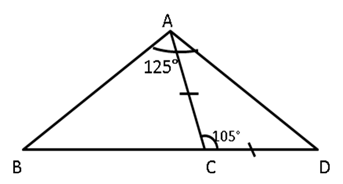
Question 8

In ABC, BC produced to D, such that, AC = CD; ∠BAD = 125^o and ∠ACD = 105^o. Show that BC > CD.

Solution 8

 

Question 9

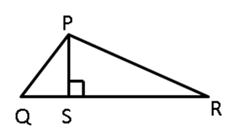
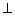In PQR, PSQR ; prove that:

PQ > QS and PQ > PS

Solution 9

 

Question 10

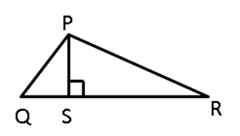
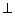In PQR, PSQR ; prove that:

PR > PS

Solution 10

 

Question 11

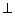In PQR, PSQR ; prove that:

PQ + PR > QR and PQ + QR >2PS.

Solution 11

 

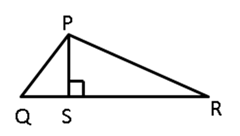
Question 12

In the given figure, T is a point on the side PR of triangle PQR. Show that

a. PT < QT

b. RT < QT

Solution 12

 

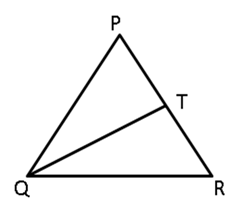
Question 13

In PQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.

Solution 13

 

Question 14

Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.

Solution 14

 

 

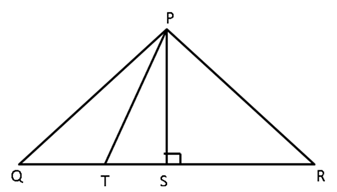
Question 15

ABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.

Solution 15

 

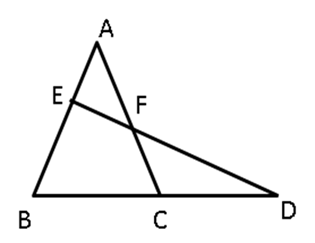
Question 16

In ABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.

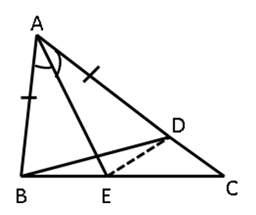
Solution 16

 

Question 17

In ABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.

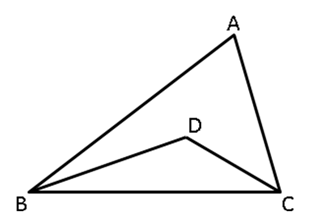
Solution 17

 

 

Question 18

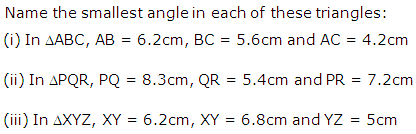
Solution 18

Question 19

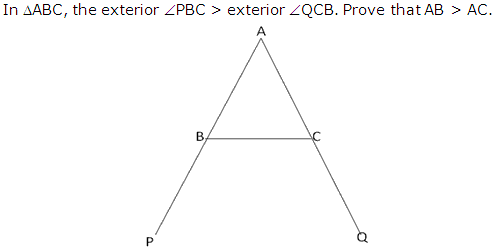
Solution 19

Question 20

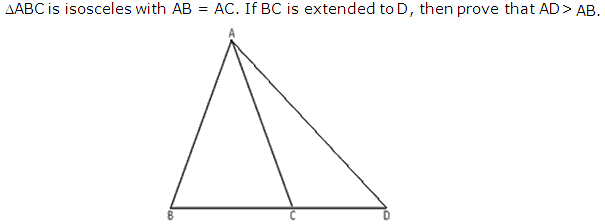
Solution 20

Question 21

Solution 21

Question 22

Solution 22

Question 23

Solution 23

Question 24

Solution 24

Question 25

Solution 25

Question 26

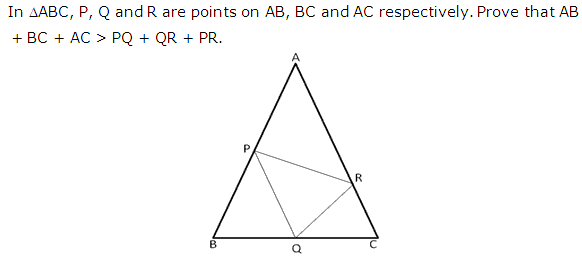
Solution 26

Question 27

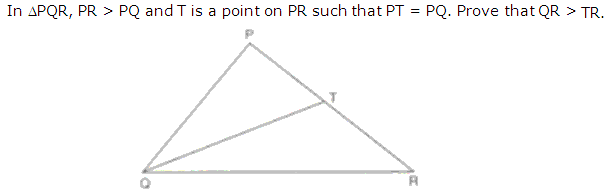
Solution 27

Question 28

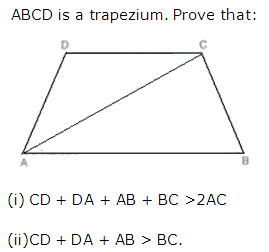
Solution 28