FRANK Solutions for Class 9 Maths Chapter 17 - Pythagoras Theorem

Chapter 17 - Pythagoras Theorem Exercise Ex. 17.1

Question 1

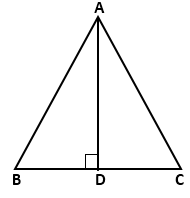
InABC, AD is perpendicular to BC. Prove that

AB² + CD² = AC² + BD²

Solution 1

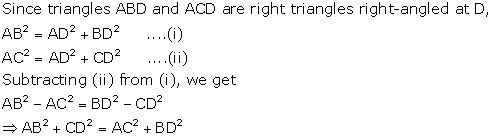
Question 2

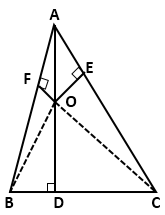
From a point O in the interior of aABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that:

a. AF² + BD² + CE² = OA² + OB² + OC² - OD² - OE² - OF²

b. AF² + BD² + CE² = AE² + CD² + BF²

Solution 2

Question 3

In a triangle ABC, AC > AB, D is the midpoint BC, and AEBC. Prove that:

 

Solution 3

Question 4

 

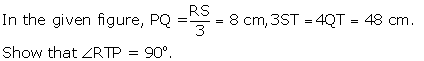
Solution 4

Question 5

Ina right-angled triangle ABC,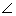ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.

Solution 5

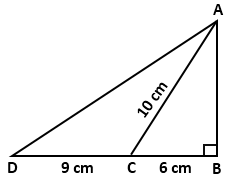
Question 6

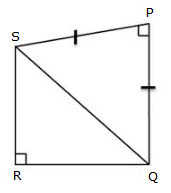
In the given figure. PQ = PS, 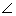P =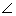R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.

Solution 6

Question 7

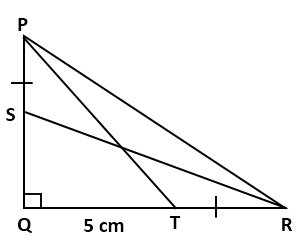
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.

Solution 7

Question 8

PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.

Solution 8

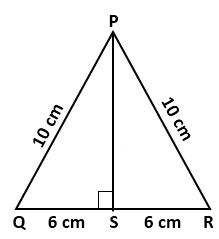
Question 9

In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.

Solution 9

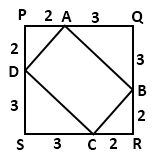
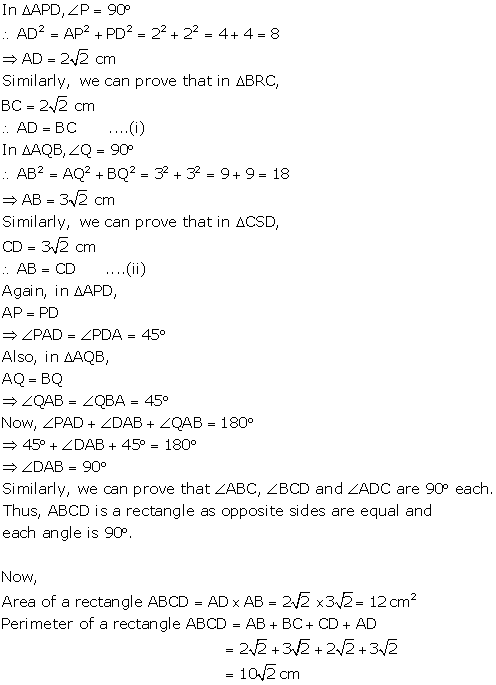
Question 10

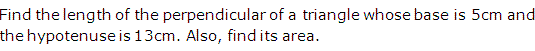
Solution 10

Question 11

Solution 11

Question 12

Solution 12

Question 13

Solution 13

Question 14

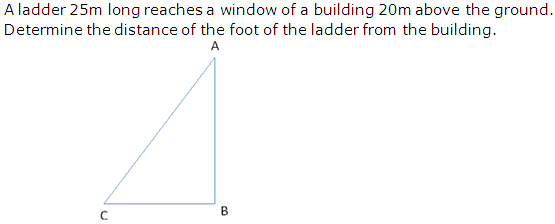
Solution 14

Question 15

 

Solution 15

Question 16

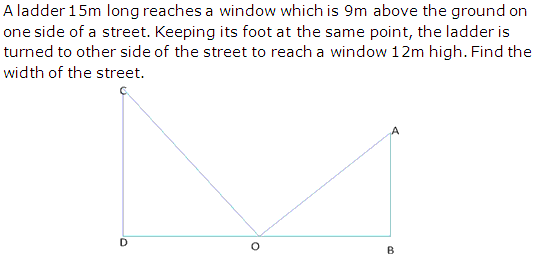
Solution 16

Question 17

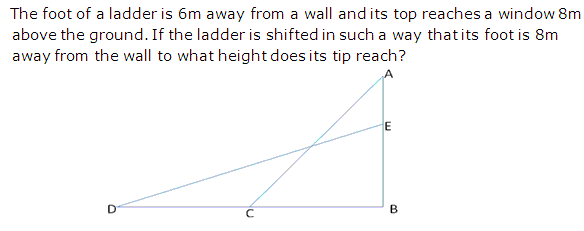
Solution 17

Question 18

Solution 18

Question 19

Solution 19

Question 20

Solution 20

Question 21

Solution 21

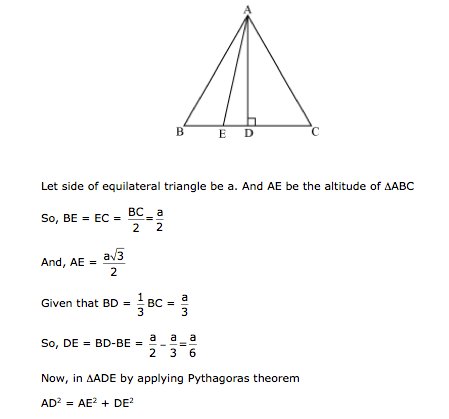
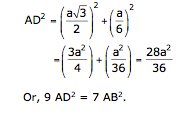
Question 22

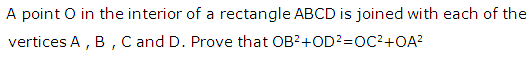
Solution 22

Question 23

Solution 23

Question 24

Solution 24

Question 25

Solution 25

Question 26

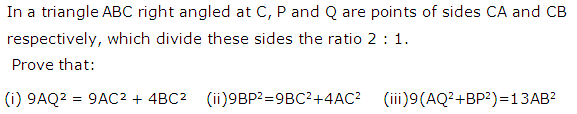
Solution 26