FRANK Solutions for Class 10 Physics Chapter 1.4 - Work, Energy, Power and Their Relation with Force

Chapter 1.4 - Work, Energy, Power and Their Relation with Force Exercise 37

Question 1

Work is the application of a ....... through a distance.

Solution 1

Force

Question 2

A boy does work when he pushes against a brick wall. (yes/no).

Solution 2

Yes

Question 3

What is the SI unit of work?

Solution 3

Joule

Question 4

Nm is the unit of .......

Solution 4

Work

Question 5

One joule is the amount of work done when a force of ......... moves a body through a distance of .......

Solution 5

1N, 1m in its own direction

Question 6

What is the work done when no net force is applied on the body?

Solution 6

When no net force is applied, the work done which is the dot product of force and displacement is zero.

Chapter 1.4 - Work, Energy, Power and Their Relation with Force Exercise 38

Question 1

What is the work done when the displacement of the body is in the opposite direction to that of the applied force?

Solution 1

Question 2

What is the work done by the gravitational force of the earth on a satellite revolving around the earth?

Solution 2

The work done by the gravitational force of the earth on a satellite revolving around the earth is zero because the motion of the satellite is perpendicular to the force at every point.

Question 3

What is the work when a load of 500 kg is lifted vertically by 5 m? Given, g = 10 ms^-2. Express your answer in kilo joule.

Solution 3

Question 4

A man lifts a mass of 10 kg from the floor to a shelf 4 meter high. If g = 10 ms^-2, what is the work done?

Solution 4

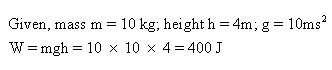
Question 5

What is the work done against gravity when a body is moved horizontally along a frictionless surface?

Solution 5

The work done against gravity is zero when a body is moved horizontally along a frictionless surface because the force of gravity is perpendicular to the displacement in this case.

Question 6

What do you mean by the term 'work'?

Solution 6

'Work' is said to be done when the applied force makes the body move i.e., there is a displacement of body.
It is equal to the product of force and the displacement of the point of application of the force in the direction of force.

Question 7

What are the quantities on which the work done depends?

Solution 7

Work done depends upon:
(i) the magnitude and direction of the applied force, and
(ii) the displacement it produces.

Question 8

When you move upstairs, do you perform some work?

Solution 8

Yes, we perform work against gravity.

Question 9

What should be the angle between the directions of the displacement and the applied force so that the work done is zero?

Solution 9

The angle should be 90^o.

Question 10

Why is the work done on an object moving along a circular path zero?

Solution 10

This is because at each point of the circular path, the displacement is perpendicular to the force, which is directed towards the centre, along the radius.

Question 11

In which one of the following cases is the work done more?  When the angle between the direction of motion and that of the force is (i) 90°     (ii) 0°.

Solution 11

When the angle between the direction of motion and that of the force is 90°;
W = Fd cos 90° = 0
When the angle between the direction of motion and that of the force is 0°;
W = Fd cos 0° = Fd
Hence in the second case, when the angle is 0°; the work done is more.

Question 12

A man carrying a suitcase in his hand is walking horizontally. What is the work done against gravity?

Solution 12

The displacement of the man and suitcase is along the horizontal direction. Thus, the angle between the displacement and the force of gravity is 90°;
Thus, W = Fd cos 90° = 0
Hence, no work is done against gravity in this case.

Question 13

What is the work done on a body by the gravitational force towards the centre of the path acting when it moves along a circular path?

Solution 13

When a body moves along a circular path, work done by the gravitational force towards the centre of the path is zero, because the displacement in this case is normal to the gravitational force.

Question 14

What is the work done on the earth by the gravitational force of the sun during its motion around the sun?

Solution 14

The work done by the gravitational force of the sun on earth during its motion around the sun is zero because at every point, the displacement of earth is perpendicular to the gravitational force of sun i.e.,
 W = Fd cos 90⁰ = 0

Question 15

What do you mean by a kilo joule?

Solution 15

A kilojoule of work is said to done when a force of 1 newton displaces a body through 1000 metres in its own direction.
1 kJ = 10³ joules

Question 16

How many joules are there in 1 mega joule?

Solution 16

1 MJ = 10⁶ joules

Question 17

Define 'joule'.

Solution 17

The SI unit of work is joule.
1 joule of work is said to be done when a force of 1 newton displaces a body through 1 metre in its own direction.

Question 18

What is the ratio of SI units to CGS units of 'work'?

Solution 18

The SI unit of work is 'joules' and the CGS unit is 'erg'.
1 joule = 10⁷ erg
Thus the ratio is 10⁷: 1

Question 19

An engine does 54,000 J of work by exerting a force of 6000 N on it. What is the displacement in the direction of the force?

Solution 19

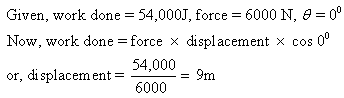
Question 20

How much force is applied on a body when 150 J of work is done in displacing the body through a distance of 10 m in the direction of the force?

Solution 20

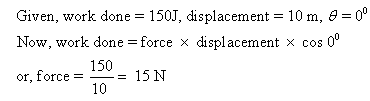
Question 21

Work done by a force is equal to the product of ....... and ....

Solution 21

Applied force, displacement in the direction of the applied force.

Question 22

Give two examples of work done.

Solution 22

Examples of work done:
(i) In free fall of a body of mass m, under gravity from a height h, the force of gravity (F=mg) is in the direction of displacement (=h) and the work done by the gravity is mgh.
(ii) A coolie lifting a load does work against gravity.

Question 23

On what factors does the work done by a force depend?

Solution 23

Work done depends upon:
(i) the magnitude and direction of the applied force, and
(ii) the displacement it produces.

Question 24

Write an expression for work done by a force depends?

Solution 24

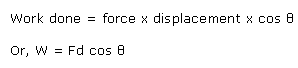
Question 25

Write an expression for the work done against gravity.

Solution 25

Work done against gravity = mass x acceleration due to gravity x height
Or, W = mgh

Question 26

No work is done by a man moving on a horizontal road while carrying a box on his head. Explain.

Solution 26

The displacement of the man and box is along the horizontal direction. Thus, the angle between the displacement and the force of gravity is 90⁰;
Thus, W = Fd cos 90⁰ = 0
Hence, no work is done against gravity in this case; however some work is done against friction.

Question 27

Is power a scalar quantity?

Solution 27

Yes, power is a scalar quantity.

Question 28

Can every force produce work?

Solution 28

No, every force cannot produce work. Force can produce work if the applied force cause displacement in the direction of the force.

Question 29

Distinguish between work and power.

Solution 29

Work is said to be done only when the applied force on a body makes the body move but power is the rate of doing work.
The SI unit of work is 'joules' and that of power is 'watt'.

Question 30

Complete the following sentences:
(a)    The SI unit of work is ....... and of power is .......
(b)    Kilowatt is the unit of ....... and kWh is the unit of
(c)    Joule is the unit of .......
(d)    1 J = ........ Erg.
(e)    1 H.P. = ........ W.

Solution 30

(a) joule, watt
(b) power, energy
(c) work
(d) 10⁷
(e) 746

Question 31

A weight lifted a load of 200 kgf to a height of 2.5 m in 5 s. calculate: (i) the work done, and (ii) the power developed by him. Take g= 10 N kg^-1.

Solution 31

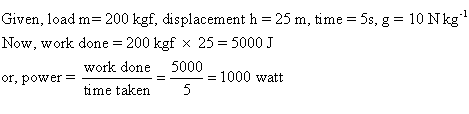
Question 32

What is the work done when the object acted upon by a force remains at rest?

Solution 32

The work done is zero because the displacement is zero.

Question 33

What is the work done when the force on the object and the displacement of the object are perpendicular to each other?

Solution 33

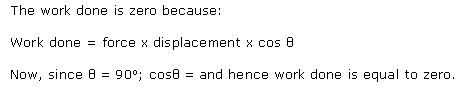
Question 34

Is work done a scalar or a vector physical quantity?

Solution 34

Work is a scalar quantity because it is a measure of transfer of energy without indicating any direction.

Chapter 1.4 - Work, Energy, Power and Their Relation with Force Exercise 39

Question 1

A boy of mass m climbs up a staircase of vertical height h. What is the work done by the boy against the force of gravity? What would have been the work done if he uses a lift in climbing the same vertical height?

Solution 1

Work done depends upon the vertical height and not the path taken, hence if the boy uses a lift to reach the same vertical height, work done will be mgh.

Question 2

Can work done be zero even if force acts on the body?

Solution 2

Yes, for e.g. if you push a wall, you apply force on it but no work is done since the displacement is zero.

Question 3

What is the relation between 1 H.P. and 1 kW?

Solution 3

1 H.P. = 0.746 kW

Question 4

It takes 20 s for A to climb up the stairs, while B does the same in 15 s. compare the (i) work done, and (ii) power developed by A and B.

Solution 4

Question 5

State and define the SI unit of power.

Solution 5

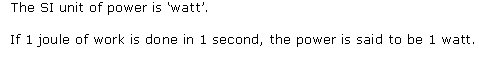
Question 6

Write the SI and CGS units of power. How are they related?

Solution 6

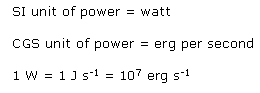
Question 7

A machine raises a load of 750 N through a height of 16 m in 5s. calculate:
(i)    work done by machine,
(ii)    power at which the machine works.

Solution 7

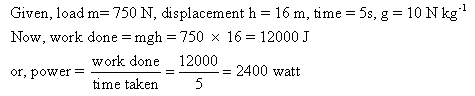
Question 8

Name the physical quantity whose MKS units are kgm²s^-3.

Solution 8

Power